O valor Z é uma estatística de teste para testes Z que mede a diferença entre uma estatística observada e seu parâmetro de população em unidades de erro padrão. Por exemplo, uma seleção de moldes de fábrica possui profundidade média de 10 cm e desvio padrão de 1 cm. Um molde com profundidade de 12 cm possui valor Z de 2, porque sua profundidade é dois desvios padrão maior que a média. A linha vertical representa essa observação, e seu local em relação a toda a população:
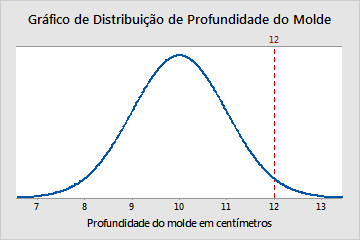
A conversão de uma observação para um valor de Z é chamada de padronização. Para padronizar uma observação em uma população, subtraia a média da população a partir da observação de interesse e divida o resultado pelo desvio padrão da população. O resultado destes cálculos é o valor de Z associado com a observação de interesse.
É possível usar um valor de Z para determinar se a hipótese nula deve ser rejeitada. Para determinar se deve rejeitar a hipótese nula, compare o valor de Z em seu valor crítico, que pode ser encontrado em uma tabela normal padrão na maioria dos livros de estatísticas. O valor crítico é Z1-α/2 para um teste bilateral e Z1-α para um teste unilateral. Se o valor absoluto do valor Z for maior do que o valor crítico, você deve rejeitar a hipótese nula. Caso contrário, você não deve rejeitar a hipótese nula.
Por exemplo, você quer saber se um segundo grupo de moldes também tem uma profundidade média de 10 centímetros. Você mede a profundidade de cada molde no segundo grupo e calcular a profundidade média do grupo. Um teste Z para 1 amostra calcula um valor de Z de -1,03. Você escolhe um α de 0,05, o que resulta num valor crítico de 1,96. Como o valor absoluto do valor de Z é menor que 1,96, você não deve rejeitar a hipótese nula e não é possível concluir que a profundidade média do molde é diferente de 10 centímetros.
