Os graus de liberdade (DF) são a quantidade de informação que seus dados fornecem que você pode "gastar" para estimar os valores de parâmetros populacionais desconhecidos, e calcular a variabilidade dessas estimativas. Esse valor é determinado pelo número de observações em sua amostra e o número de parâmetros em seu modelo.
Aumentar seu tamanho amostral fornece mais informações sobre a população e, desta forma, aumenta os graus de liberdade em seus dados. Adicionar parâmetros ao seu modelo (aumentando o número de termos em uma equação de regressão, por exemplo) "gasta" informações dos seus dados, e reduz os graus de liberdade disponíveis para estimar a variabilidade das estimativas de parâmetro.
Graus de liberdade também são usados para caracterizar uma distribuição específica. Diversas famílias de distribuições, como t, F e qui-quadrado, usam graus de liberdade para especificar qual distribuição específica t, F ou qui-quadrado é apropriada pra diferentes tamanhos amostrais e diferentes números de parâmetros modelo. Por exemplo, a seguinte figura descreve as diferenças entre distribuições qui-quadrado com diferentes graus de liberdade.
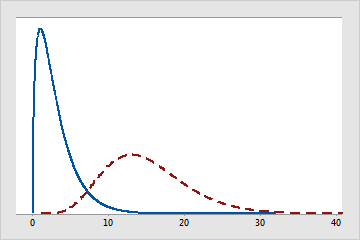
Distribuições qui-quadrado com diferentes graus de liberdade
A distribuição de linha sólida tem 3 graus de liberdade. A distribuição de linha tracejada tem 15 graus de liberdade.
Exemplos
Por exemplo, o teste t para 1 amostra estima apenas um parâmetro: a média populacional. O tamanho amostral de n constitui n informações para estimativa da média populacional e sua variabilidade. Um grau de liberdade é gasto estimando-se a média, e os n-1 graus de liberdade restantes estimam a variabilidade. Portanto, um teste t para 1 amostra usa uma distribuição t com n-1 graus de liberdade.
Por outro lado, a regressão linear múltipla deve estimar uma parâmetro para cada termo que você escolha incluir no modelo, e cada um consome um grau de liberdade. Portanto, incluir termos em excesso em um modelo de regressão linear múltipla reduz os graus de liberdade disponíveis para estimar a variabilidade dos parâmetros, e pode torná-lo menos confiável.
