O que são parâmetros, estimativas de parâmetros e distribuições de amostragem?

Quando você quer determinar informações sobre uma característica específica da população (por exemplo, a média), normalmente você extrai uma amostra aleatória daquela população, porque é inviável medir toda a população. Usando esse exemplo, você calcula a característica da amostra correspondente, que é usada para resumir as informações sobre a característica desconhecida da população. A característica de interesse da população é chamada de parâmetro e a característica da amostra correspondente é a estatística da amostra ou parâmetro de estimativa. Como a estatística é um resumo das informações sobre um parâmetro obtido a partir da amostra, o valor de uma estatística depende da amostra particular que foi extraída da população. Os seus valores mudam aleatoriamente a partir de uma amostra aleatória para a seguinte, por conseguinte, uma estatística é uma quantidade aleatória (variável). A distribuição de probabilidade desta variável aleatória é chamada distribuição amostral. A distribuição amostral de uma (amostra) estatística é importante porque nos permite tirar conclusões sobre o parâmetro de população correspondente com base em uma amostra aleatória.

Por exemplo, quando extraímos uma amostra aleatória de uma população distribuída normalmente, a média da amostra é uma estatística. O valor da média da amostra com base na amostra em questão é uma estimativa da média da população. Este valor estimado irá mudar aleatoriamente se uma amostra diferente for extraída da mesma população normal. A distribuição de probabilidade que descreve essas mudanças é a distribuição amostral da média da amostra. A distribuição amostral de uma estatística especifica todos os possíveis valores de uma estatística e a frequência com que algum intervalo de valores da estatística ocorre. No caso em que a população de origem for normal, a distribuição de amostragem da média da amostra também é normal.

As seções a seguir fornecem mais informações sobre parâmetros, estimativas de parâmetros e distribuições amostrais.

Sobre parâmetros

Os parâmetros são medidas descritivas de toda uma população que podem ser usadas como entradas para uma função de distribuição de probabilidade (FDP) para gerar curvas de distribuição. Os parâmetros são normalmente representados por letras gregas para distingui-los de estatísticas amostrais. Por exemplo, a média populacional é representada pela letra grega mu (μ) e o desvio padrão da população pela letra grega sigma (σ). Os parâmetros são constantes fixas, isto é, eles não variam como as variáveis. Contudo, seus valores são normalmente desconhecidos, porque é inviável medir uma população inteira.

Cada distribuição é inteiramente definida por diversos parâmetros específicos, normalmente entre um e três. A tabela a seguir fornece exemplos dos parâmetros necessários para três distribuições. Os valores de parâmetro determinam o local e a forma da curva da distribuição do gráfico, e cada combinação exclusiva de valores de parâmetro produzem uma curva de distribuição exclusiva.

Distribuição	Parâmetro 1	Parâmetro 2	Parâmetro 3
Qui-quadrado	Graus de liberdade
Normal	Média	Desvio padrão
Gama de 3 parâmetros	Forma	Escala	Limite

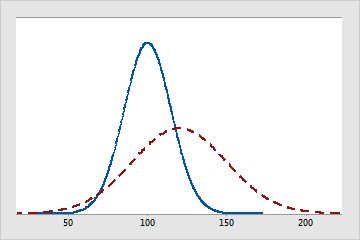
Por exemplo, uma distribuição normal é definida por dois parâmetros, a média e o desvio padrão. Se esses forem especificados, toda a distribuição será precisamente conhecida.

A linha sólida representa uma distribuição normal com uma média de 100 e um desvio padrão de 15. A linha pontilhada também é uma distribuição normal, mas ela tem uma média de 120 e um desvio padrão de 30.

Sobre as estimativas de parâmetro (também chamadas de estatísticas de amostra)

Os parâmetros são medidas descritivas de toda uma população. Contudo, seus valores são normalmente desconhecidos, porque é inviável medir uma população inteira. Por causa disso, é possível extrair uma amostra aleatória da população para obter estimativas de parâmetros. Um dos objetivos das análises estatísticas é a obtenção das estimativas dos parâmetros da população, juntamente com a quantidade de erro associada a essas estimativas. Essas estimativas também são conhecidas como estatísticas de amostra.

Existem diversos tipos de estimativas de parâmetros:

As estimativas pontuais são o valor único e mais provável de um parâmetro. Por exemplo, a estimativa pontual da média da população (o parâmetro) é a média da amostra (a estimativa do parâmetro).
Intervalos de confiança são uma faixa de valores que provavelmente contém o parâmetro da população.

Para um exemplo de estimativas de parâmetros, suponha que você trabalha para um fabricante de velas de ignição que está estudando um problema na folga de sua vela de ignição. Seria muito caro para medir cada vela de ignição fabricada. Em vez disso, você faz uma amostragem aleatória de 100 velas de ignição e mede a folga em milímetros. A média da amostra é 9,2. Esta é a estimativa pontual para a média da população (μ). Você também pode criar um intervalo de confiança de 95% para μ que é (8,8, 9,6). Isso significa que você pode ter 95% de certeza de que o verdadeiro valor da folga média para todas as velas de ignição é entre 8,8 e 9,6.

Sobre as distribuições de amostras

Uma distribuição de amostragem é a distribuição de probabilidade de um determinado estatística, como a média. Para ilustrar a distribuição amostral, vamos examinar um exemplo simples onde a população total é conhecida. Por exemplo, a tabela a seguir mostra os pesos de toda a população de 6 abóboras. As abóboras só podem ser um dos valores de peso listados na tabela a seguir.

Abóbora	1	2	3	4	5	6
Peso	19	14	15	12	16	17

Apesar de toda a população ser conhecida, para fins ilustrativos, tomamos todas as amostras aleatórias possíveis da população que contêm 3 abóboras (20 amostras aleatórias). Em seguida, calcula-se a média de cada amostra. A distribuição de amostras para a média da amostra é descrita por todas as médias de amostra, para cada amostra aleatória possível de 3 abóboras, o qual é mostrado na tabela a seguir.

Amostra	Pesos	Ponderação da média	Probabilidade
2, 3, 4	14, 15, 12	13,7	1/20
2, 4, 5	14, 12, 16	14	1/20
2, 4, 6	14, 12, 17	14,3	2/20
3, 4, 5	15, 12, 16	14,3	2/20
3, 4, 6	15, 12, 17	14,7	1/20
1, 2, 4	19, 14, 12	15	3/20
2, 3, 5	14, 15, 16
4, 5, 6	12, 16, 17
2, 3, 6	14, 15, 17	15,3	2/20
1, 3, 4	19, 15, 12	15,3	2/20
1, 4, 5	19, 12, 16	15,7	2/20
2, 5, 6	14, 16, 17	15,7	2/20
1, 2, 3	19, 14, 15	16	3/20
3, 5, 6	15, 16, 17
1, 4, 6	19, 12, 17
1, 2, 5	19, 14, 16	16,3	1/20
1, 2, 6	19, 14, 17	16,7	2/20
1, 3, 5	19, 15, 16	16,7	2/20
1, 3, 6	19, 15, 17	17	1/20
1, 5, 6	19, 16, 17	17,3	1/20

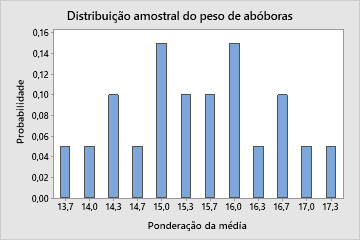
A distribuição amostral dos pesos médios é mostrada neste gráfico. A distribuição é centralizada em torno de 15,5, que é também o valor verdadeiro para a média da população. E as amostras aleatórias com médias de amostra mais próximas de 15,5 têm uma maior probabilidade de ocorrer do que as amostras com as médias de amostra mais distantes de 15,5.

Na prática, é proibitivo e impraticável tabular a distribuição da distribuição de amostragem como no exemplo ilustrativo acima. Mesmo no melhor cenário em que você conheça a população de origem de suas amostras, talvez você não possa determinar a distribuição amostral exata da amostra estatística de interesse. No entanto, em alguns casos, é possível que você consiga aproximar a distribuição amostral da amostra estatística. Por exemplo, se você extrair amostra da população normal e, em seguida, a média da amostra tiver exatamente a distribuição normal.

Mas se você extrair a amostra de uma população diferente de população normal, talvez não seja capaz de determinar a distribuição exata da média da amostra. No entanto, por causa do teorema central do limite, a média da amostra é aproximadamente distribuída como normal, desde que suas amostras sejam grandes o suficiente. Então, se a população for desconhecida e suas amostras sejam grandes o suficiente, talvez você possa dizer, por exemplo, que há aproximadamente 85% de certeza de que a média da amostra esteja dentro de um determinado número de desvios padrão da média da população.