O teorema central do limite é um teorema fundamental de probabilidade e estatísticas. O teorema descreve a distribuição da média de uma amostra aleatória de uma população com variância finita. Quando o tamanho amostral é suficientemente grande, a distribuição da média é uma distribuição aproximadamente normal. O teorema aplica-se independentemente da forma da distribuição da população. Muitos procedimentos estatísticos comuns requerem que os dados sejam aproximadamente normais. O teorema central do limite permite a aplicação destes procedimentos úteis a populações que são fortemente não-normais. Quão grande o tamanho amostral deve ser depende da forma da distribuição original. Se a distribuição da população for simétrica, um tamanho amostral de 5 poderia render uma boa aproximação. Se a distribuição da população for fortemente assimétrica, será necessária uma amostra maior. Por exemplo, a distribuição da média pode ser aproximadamente normal, se o tamanho amostral for maior do que 50. Os gráficos a seguir mostram exemplos de como a distribuição afeta o tamanho amostral de que você precisa.
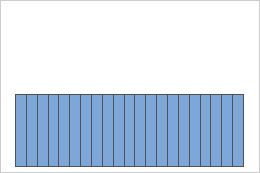
Distribuição uniforme
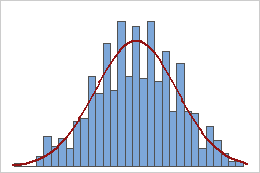
Médias amostrais
Amostras de uma população uniforme
Uma população que segue uma distribuição uniforme é simétrica, mas fortemente não-normal, como mostra o primeiro histograma. Contudo, a distribuição de médias amostrais de 1000 amostras de tamanho 5 desta população é aproximadamente normal devido ao teorema central do limite, como mostra o segundo histograma. Este histograma de médias amostrais inclui uma curva normal sobreposta para ilustrar sua normalidade.
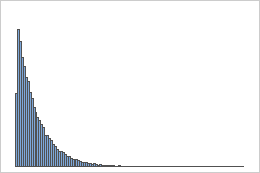
Distribuição exponencial
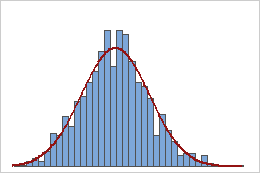
Médias amostrais
Amostras de uma população exponencial
Uma população que segue uma distribuição exponencial é assimétrica e não-normal, como mostra o primeiro histograma. Contudo, a distribuição de médias amostrais de 1000 amostras de tamanho 50 desta população é aproximadamente normal devido ao teorema central do limite, como mostra o segundo histograma. Este histograma de médias amostrais inclui uma curva normal sobreposta para ilustrar sua normalidade.
