Um valor crítico é um ponto sobre a distribuição da estatística de teste sob a hipótese nula que define um conjunto de valores que chama para rejeitar a hipótese nula. Este conjunto é chamado região crítica ou de rejeição. Normalmente, os testes unilaterais têm um valor crítico e os testes bilaterais têm dois valores críticos. Os valores críticos são determinadas de modo a que a probabilidade de que o teste estatístico tenha um valor na região de rejeição do teste quando a hipótese nula é verdadeira é igual ao nível de significância (denotado como α ou alfa).
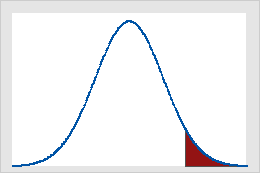
Figura A
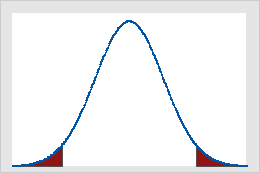
Figura B
Valores críticos na distribuição normal padrão para alfa = 0,05
A Figura A mostra que os resultados de um teste-Z unicaudal são significativos se o valor da estatística de teste for igual a ou maior do que 1,64, o valor crítico neste caso. A área sombreada representa a probabilidade de um erro de tipo I (α = 5% neste exemplo) para a área sob a curva. A Figura B mostra que os resultados de um teste Z de duas caudas são significativos se o valor absoluto da estatística de teste for igual a ou maior do que 1,96, o valor crítico neste caso. As duas áreas sombreadas somam até 5% (α) da área sob a curva.
Exemplos de cálculo de valores críticos
Em testes de hipóteses, existem duas maneiras de determinar se existe evidência suficiente na amostra para rejeitar H0 ou para deixar de rejeitar H0. A maneira mais comum é comparar o valor-p com um valor pré-especificado de alfa, em que alfa é a probabilidade de rejeitar H0 quando H0 é verdadeiro. No entanto, uma abordagem equivalente é comparar o valor calculado da estatística de teste com base em seus dados com o valor crítico. A seguir estão exemplos de como calcular o valor crítico para um teste t com 1 amostra e uma ANOVA com um fator.
Cálculo de um valor crítico para um teste t com 1 amostra
- Selecione .
- Selecione Probabilidade acumulada inversa.
- Em Graus de liberdade, insira 9 (o número de observações menos um).
- Em Constante de entrada, insira 0,95 (um menos metade de alfa).
Isso fornece a probabilidade acumulada, que é igual ao valor crítico de 1,83311. Se o valor absoluto da estatística t for maior que este valor crítico, você rejeita a hipótese nula, H0, no nível de significância 0,10.
Cálculo de um valor crítico para uma análise de variância (ANOVA)
- Escolha .
- Selecione Probabilidade acumulada inversa.
- Em Graus de liberdade do numerador, insira 2 (o número de níveis de fator menos um).
- Em Graus de liberdade do denominador, insira 9 (os graus de liberdade para o erro).
- Em Constante de entrada, insira 0,95 (um menos alfa).
Isso fornece a probabilidade acumulada, que é igual ao valor crítico de 4,25649. Se a estatística F for maior que este valor crítico, você rejeita a hipótese nula, H0, no nível de significância 0,05.
