Ao avaliar a relação entre duas variáveis, é importante determinar como as variáveis estão relacionadas. Relações lineares são mais comuns, mas as variáveis também podem ter uma relação não linear ou monotônica, como mostrado abaixo. Também é possível que não haja nenhuma relação entre as variáveis. Você deve começar criando um gráfico de dispersão das variáveis para avaliar a relação.
Uma relação linear é uma tendência nos dados que pode ser modelada por uma linha reta. Por exemplo, suponha que uma empresa aérea deseja estimar o impacto do preço dos combustíveis sobre o custo dos voos. Eles determinam que, para cada aumento de um dólar no preço de um galão de gasolina de aviação, o custo do voo Los Angeles-New York aumenta em torno de US$ 3500. Isso descreve uma relação linear entre o custo do combustível de aviação e o custo do voo.
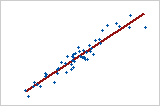
Gráfico 1: Relação linear positiva forte
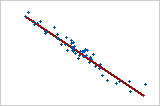
Gráfico 2: Relação linear negativa forte
Quando as duas variáveis aumentam ou diminuem simultaneamente, e a uma taxa constante, existe uma relação linear positiva. Os pontos no Gráfico 1 seguem mais perto da linha, sugerindo que a relação entre as variáveis é forte. O coeficiente de Pearson para essa relação é +0,921.
Quando uma variável aumenta e a outra variável diminui, existe uma relação linear negativa. Os pontos no Gráfico 2 seguem mais perto da linha, sugerindo que a relação entre as variáveis é forte. O coeficiente de correlação de Pearson para essa relação é 0,968.
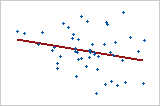
Gráfico 3: relação linear fraca
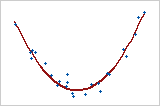
Gráfico 4: Relação não linear
Os pontos de dados no Gráfico 3 parecem estar distribuídos aleatoriamente. Eles não estão próximos da linha, indicando uma relação fraca, se existir. O coeficiente de correlação de Pearson para essa relação é -0,253.
Se uma relação entre duas variáveis não é linear, a taxa de aumento ou diminuição pode mudar como uma mudança de variáveis, causando um "padrão curvo" nos dados. Esta tendência curva pode ser melhor modelada por uma função não linear, como uma função quadrática ou cúbica ou ser transformada para tornar mais linear. O Gráfico 4 mostra uma relação forte entre duas variáveis. Entretanto, como a relação não é linear, o coeficiente de correlação de Pearson é apenas +0,244. Essa relação ilustra o porquê é importante traçar os dados para explorar quaisquer relações que possam existir.
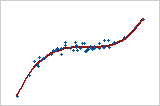
Gráfico 5 relação monotônica
Em uma relação monotônica, as variáveis tendem a mover-se na mesma direção relativa, mas não necessariamente a uma taxa constante. Em uma relação linear, as variáveis se movem na mesma direção, a uma taxa constante. O Gráfico 5 mostra as duas variáveis aumentando simultaneamente, mas não à mesma taxa. A relação é monotônica porém não linear. O coeficiente de correlação de Pearson para esses dados é 0,843, mas a correlação de Spearman é maior, 0,948.
Relações lineares também são monotônicas. Por exemplo, a relação mostrada no Gráfico 1 é monotônica e linear.
