Neste tópico
Etapa 1: Determine um intervalo de confiança para a diferença da média da população
Primeiro, considere a diferença média e depois examine o intervalo de confiança. A diferença média é a média das diferenças entre as observações pareadas na amostra.
A diferença média é uma estimativa da diferença média da população. Como a diferença média está baseada em dados das amostras e não na população total, é improvável que a diferença da média da amostra seja igual à diferença média da população. Para estimar melhor a diferença da média da população, use o intervalo de confiança da diferença.
O intervalo de confiança fornece um intervalo de valores possíveis para a diferença da média da população das observações pareadas. Por exemplo, um nível de confiança de 95% indica que, se você extrair 100 amostras aleatórias da população, poderia esperar que, aproximadamente, 95 das amostras produza intervalos que contêm a diferença média da população. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra. Para obter mais informações, vá para Como obter um intervalo de confiança mais preciso.
Estimativa da diferença pareada
| Média | DesvPad | EP Média | IC de 95% da diferença_µ |
|---|---|---|---|
| 2,200 | 3,254 | 0,728 | (0,677; 3,723) |
Principais resultados: Diferença média, IC de 95% para diferença média
Nesses resultados, a estimativa da diferença da média da população em pulsações é de 2,2. Você pode ter 95% de confiança e que a diferença média da população está entre 0,677 e 3,723.
Etapa 2: Determine se os resultados de teste são estatisticamente significativos
- Valor de p ≤ α: A diferença entre as médias é estatisticamente significativa (rejeite H0)
- Se o valor de p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula. É possível concluir que a diferença entre as médias da população não é igual à diferença hipotética. Se você não especificar uma diferença hipotética, o Minitab testa se não há diferença entre as médias (Diferença hipotética = 0) Use seu conhecimento especializado para determinar se a diferença é praticamente significativa. Para obter mais informações, acesse Significância estatística e prática.
- Valor de p > α: A diferença entre as médias não é estatisticamente significativa (não deve rejeitar H0)
- Se o valor de p for maior do que o nível de significância, você não deve rejeitar a hipótese nula. Não há evidências suficientes para concluir que a diferença média entre as observações pareadas é estatisticamente significativa. Certifique-se de que o teste tenha poder suficiente para detectar uma diferença que seja significativa na prática. Para obter mais informações, acesse Poder e tamanho de amostra para teste t pareado.
Teste
| Hipótese nula | H₀: diferença_μ = 0 |
|---|---|
| Hipótese alternativa | H₁: diferença_μ ≠ 0 |
| Valor-T | Valor-p |
|---|---|
| 3,02 | 0,007 |
Resultados principais: valor-p
Nestes resultados, a hipótese nula afirma que a diferença média da frequência cardíaca em repouso para pacientes antes e após um programa de corrida é 0. Como o valor-p é 0,007, o que é menor do que o nível de significância de 0,05, a decisão é rejeitar a hipótese nula e concluir que existe uma diferença na frequência cardíaca de pacientes antes e depois da execução de um programa de corrida.
Etapa 3: Verifique se há problemas nos dados
Problemas com os dados, como assimetrias ou outliers, podem afetar desfavoravelmente seus resultados. Use gráficos para procurar assimetrias e para identificar os outliers potenciais.
Examine a dispersão de seus dados para determinar se eles parecem ser assimétricos.
Quando os dados são assimétricos, a maior parte dos dados está localizada no lado alto ou baixo do gráfico. Frequentemente, a assimetria é mais fácil de detectar com um histograma ou boxplot.
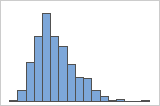
Assimétricos à direita
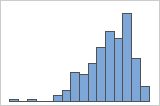
Assimétricos à esquerda
O histograma com dados assimétricos à direita mostra os tempos de espera. A maioria dos tempos de espera são relativamente curtos e apenas alguns tempos de espera são longos. O histograma com dados assimétricos à esquerda mostra os dados de tempos de falha. Alguns itens falham imediatamente e muitos outros itens falham posteriormente.
Os dados que são severamente assimétricos podem afetar a validade do valor-p se a amostra for pequena (menor que 20 valores). Se seus dados forem severamente assimétricos e você tiver uma pequena amostra, considere aumentar o tamanho amostral.
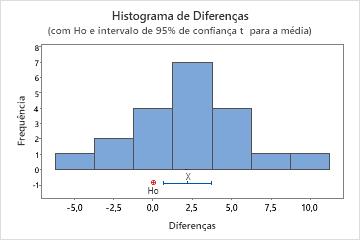
Neste histograma, os dados não parecem estar severamente assimétricos.
Identificar outliers
Outliers, que são valores de dados que estão longe dos outros valores de dados, podem afetar fortemente os resultados da análise. Geralmente, outliers são a maneira mais fácil de identificar em um boxplot.
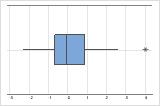
Em um boxplot, os asteriscos (*) identificam outliers.
Tente identificar a causa de todos os outliers. Corrija quaisquer erros de entrada de dados ou de medição. Considere remover valores de dados que estejam associados a eventos anormais, que ocorrem somente uma vez (também chamados de causas especiais). Em seguida, repita a análise. Para obter mais informações, acesse Identificação de outliers.
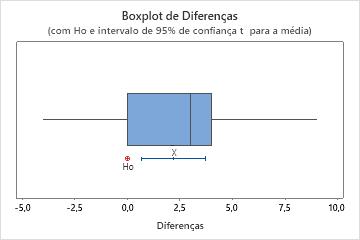
Neste boxplot, não existem outliers.
