Especifique o teste, especifique o nível de significância e selecione a hipótese alternativa.
Neste tópico
Teste de Outlier
Todos os testes de outlier do Minitab são concebidos para detectar um único outlier em uma amostra. Normalmente, o teste de Grubbs funciona bem. No entanto, se uma amostra contiver mais de um outlier potencial, o teste de Grubbs e a razão do Q de Dixon pode não ser eficaz.
- Se você não souber se os dados incluem valores atípicos, utilize o teste de Grubbs.
- Se você sabe que os seus dados incluem um ou mais outliers, use um dos testes do Dixon. Os testes de Dixon são projetados para superar o efeito de mascaramento que vários outliers potenciais podem causar.
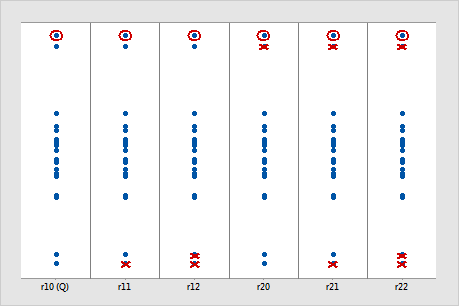
Na ilustração a seguir, cada coluna mostra como os diferentes testes de razão de Dixon tratam a mesma amostra. O valor circulado é o outlier potencial. Os Xs indicam quais valores de dados cada teste da razão de Dixon ignora quando se calcula a estatística de teste. (Esta ilustração assume que a hipótese alternativa é tanto O menor ou o maior valor dos dados é um outlier ou O maior valor dos dados é um outlier.) Para estes dados, é mais provável que o teste de razão de Dixon r22 identifique o valor circulado como um outlier.
As amostras maiores a partir de uma população normal apresentam maior probabilidade de incluir valores extremos. Dixon propôs as seguintes diretrizes gerais para as razões.
| Tamanho amostral (n) | Razão recomendada |
|---|---|
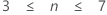 |
r10 (também chamada Q de Dixon) |
 |
r11 |
 |
r21 |
 |
r22 |
Nível de significância
Compare o nível de significância com o valor de p para decidir se deve rejeitar ou deixar de rejeitar a hipótese nula (H0). Se o valor de p for menor do que o nível de significância, a interpretação comum é que os resultados são estatisticamente significativos, e você rejeita H0.
- Escolha um nível de significância mais elevado, como 0,10, para ter mais certeza de que seja detectada qualquer possível diferença existente. Por exemplo, um engenheiro de qualidade compara a estabilidade de novos rolamentos de esferas com a estabilidade dos rolamentos atuais. Ele deve ter um alto grau de certeza de que os novos rolamentos de esferas são estáveis, porque rolamentos de esferas instáveis podem causar um desastre. O engenheiro escolhe um nível de significância de 0,10 para ter mais certeza de detectar qualquer possível diferença na estabilidade dos rolamentos de esferas.
- Escolha um nível de significância mais baixo, como 0,01, para ter mais certeza de que seja detectada apenas uma diferença que realmente existe. Por exemplo, um cientista em uma empresa farmacêutica deve ter um alto grau de certeza sobre uma afirmação de que novo medicamento da empresa reduz significativamente os sintomas. O cientista escolhe um nível de significância de 0,001 para ter mais a certeza de que qualquer diferença significativa nos sintomas realmente exista.
O que você deseja determinar? (Hipótese alternativa)
- O menor ou o maior valor dos dados é um outlier: Utilize este teste bilateral quando os menores valores de dados ou os maiores valores de dados possam ser um outlier. Este teste bilateral pode detectar outliers, tanto para os menores valores de dados quanto para os maiores, mas tem menos poder do que um teste unilateral.
- O menor valor dos dados é um outlier: Utilize este teste unilateral quando suspeitar que o menor valor dos dados é um outlier. Este teste unilateral tem maior poder do que um teste bilateral, mas não pode detectar outliers que sejam os maiores valores dos dados.
- O maior valor dos dados é um outlier: Use este teste unilateral quando suspeitar que o maior valor dos dados é um outlier. Este teste unilateral tem maior poder do que um teste bilateral, mas não pode detectar outliers que sejam os menores valores dos dados.
