Métodos e fórmulas para Teste de outlier

Por exemplo, se o outlier suspeito é o menor valor na amostra, mas a amostra inclui também dois valores atipicamente grandes, então r₁₂ é a estatística de teste apropriada. A estatística de teste r₁₀ , (também chamada de Q de Dixon), é apropriada quando a amostra inclui apenas um valor extremo.

Os valores críticos para as estatísticas dos testes de Dixon são tabulados em Rorabacher (1991).

Estatística de teste unilateral

A fórmula para o teste unilateral depende se você testar o menor valor, y_i , ou o maior valor, y_n. Para testar se y_i , é o outlier, use a seguinte fórmula:

Para testar se y_n , é o outlier, use a seguinte fórmula:

Estatística de teste bilateral

Nós definimos a estatística de teste bilateral como King (1953) define a estatística de teste bilateral relacionada com r₁₀. A estatística de teste de bilateral é dada por:

Notação

Referências

Fórmula para a estatística unilateral

Se você testar se o menor valor de dados é um outlier, então a estatística de teste G é dada por:

Se você testar se o maior valor de dados é um outlier, então a estatística de teste G é dada por:

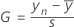
Fórmula para a estatística bilateral

Para uma hipótese bilateral, G é dado por:

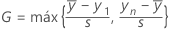
Notação

Termo	Descrição
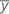	a média da amostra
yi	o io menor valor na amostra
s	o desvio padrão da amostra
n	o número de observações na amostra

Função distribuição acumulada para o teste estatístico

De acordo com Dixon (1951) e McBane (2006), as funções densidade de probabilidade da distribuição da estatística de teste r_ij pode ser escrita como:

em que C é o fator de normalização especificado por:

e a J(x,v,r) jacobiana é especificada por:

Usando a transformação onde t = (1 + r² ) v² / 2 e u² = 3x² / 2, a função de densidade pode ser reescrita como:

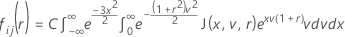
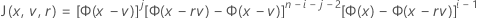
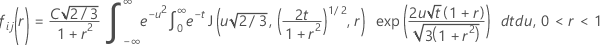
O Minitab avalia a integral interna usando uma quadratura Gauss-Laguerre de 30 pontos. O Minitab avalia a integral externa usando uma quadratura Gauss-Hermite de 30 pontos.

As funções de distribuição acumuladas para a família de estatísticas de teste são especificadas por:

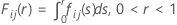
De forma semelhante a McBane (2006), o Minitab calcula F_ij(r) usando um método de quadradura de Gauss-Legendre de 16 pontos.

Valor de p para teste unilateral

Para qualquer par de índices (i, j), o valor de p para a estatística unilateral observado, R, é especificado por:

Valor de p para teste unilateral

Usando os resultados de King (1953), para qualquer par de subscritos (i, j), o valor de p para a estatística de bilateral observada, r, é especificado por:

Além disso, King observa que a aproximação acima torna-se uma igualdade para .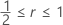

Notação

Referências

W.J. Dixon (1951). "Ratios Involving Extreme Values," Annals of Mathematical Statistics, 22(1), 68-78.

E.P. King (1953). "On Some Procedures for the Rejection of Suspected Data," Journal of the American Statistical Association, Vol. 48, No. 263, pages 531-533.

G.C. McBane (2006). "Programs to Compute Distribution Functions and Critical Values for Extreme Value Ratios for Outlier Detection," Journal of Statistical Software, Vol. 16, No. 3, pages 1-9.

Fórmula para um teste unilateral

O valor de p para um teste unilateral é:

Fórmula para um teste bilateral

O valor de p para um teste bilateral é:

Valores de p exatos versus aproximados

Se o seguinte for verdadeiro, então o valor de p é exato.

Se não, o valor de p calculado representa um limite superior para o valor de p exato. No entanto, o limite superior é uma aproximação muito boa do valor de p exato.

Notação