Neste tópico
Etapa 1: Determine se existe um outlier
- Valor de p ≤ α: Existe um outlier (rejeite H0)
- Se o valor de p é menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que existe um outlier. Tente identificar a causa de todos os outliers. Corrija quaisquer erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais).
- Valor de p > α: Não é possível concluir que existe um outlier (não deve rejeitar H0)
- Se o valor de p é maior do que o nível de significância, você não deve rejeitar a hipótese nula, porque não há evidências suficientes para concluir que existe um outlier. Você deve se certificar de que o teste tem poder suficiente para detectar um outlier. Para obter mais informações, acesse Aumentar a potência.
Método
| Hipótese nula | Todos os valores de dados são provenientes da mesma população normal |
|---|---|
| Hipótese alternativa | O menor valor dos dados é um outlier |
| Nível de significância | α = 0,05 |
Teste de Grubbs
| Variável | N | Média | DesvPad | Mín | Máx | G | P |
|---|---|---|---|---|---|---|---|
| ResistênciaÀQuebra | 14 | 123,4 | 46,3 | 12,4 | 193,1 | 2,40 | 0,044 |
Outlier
| Variável | Linha | Outlier |
|---|---|---|
| ResistênciaÀQuebra | 10 | 12,38 |
Resultados principais: P
Nestes resultados, a hipótese nula indica que todos os valores de dados provêm da mesma população normal. Como o valor de p é 0,044, que é menor do que o nível de significância de 0,05, a decisão é rejeitar a hipótese nula e concluir que existe um outlier.
Etapa 2: Determine o valor do outlier
Se o teste identificar um outlier nos dados, o Minitab exibe uma tabela de outlier. Use a tabela de outlier para determinar o valor do outlier e a linha na worksheet que contém o outlier.
Método
| Hipótese nula | Todos os valores de dados são provenientes da mesma população normal |
|---|---|
| Hipótese alternativa | O menor valor dos dados é um outlier |
| Nível de significância | α = 0,05 |
Teste de Grubbs
| Variável | N | Média | DesvPad | Mín | Máx | G | P |
|---|---|---|---|---|---|---|---|
| ResistênciaÀQuebra | 14 | 123,4 | 46,3 | 12,4 | 193,1 | 2,40 | 0,044 |
Outlier
| Variável | Linha | Outlier |
|---|---|---|
| ResistênciaÀQuebra | 10 | 12,38 |
Principais resultados: linha, outlier
Nestes resultados, o valor do outlier é 12,38 e está na linha 10.
Etapa 3: Identificar visualmente o outlier
Use o gráfico de outlier para identificar visualmente um outlier nos dados. Se existir um outlier, o Minitab o representa no gráfico como um quadrado vermelho. Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais).
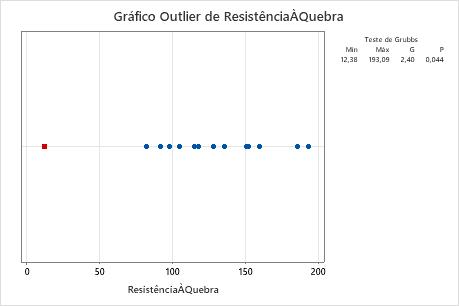
Neste gráfico de outlier, o menor valor, 12,38, é um outlier.
