Neste tópico
Hipótese nula e hipótese alternativa
- Hipótese nula
- A hipótese nula indica que todos os valores de dados provêm da mesma distribuição normal.
- Hipótese alternativa
- A hipótese alternativa indica que o menor ou o maior valor dos dados é um outlier.
Nível de significância
O nível de significância (indicado como α ou alfa) é o nível de risco máximo aceitável para rejeitar a hipótese nula quando ela é verdadeira (erro tipo I). O valor padrão é 0,05.
Interpretação
Use o nível de significância de decidir se deve rejeitar ou deixar de rejeitar a hipótese nula (H0). Se a probabilidade de que um evento ocorra for menor do que o nível de significância, a interpretação comum é que os resultados são estatisticamente significativos, e você deve rejeitar H0.
- Escolha um nível de significância mais elevado, como 0,10, para ter mais certeza de que seja detectada qualquer possível diferença existente. Por exemplo, um engenheiro de qualidade compara a estabilidade de novos rolamentos de esferas com a estabilidade dos rolamentos atuais. Ele deve ter um alto grau de certeza de que os novos rolamentos de esferas são estáveis, porque rolamentos de esferas instáveis podem causar um desastre. O engenheiro escolhe um nível de significância de 0,10 para ter mais certeza de detectar qualquer possível diferença na estabilidade dos rolamentos de esferas.
- Escolha um nível de significância mais baixo, como 0,01, para ter mais certeza de que seja detectada apenas uma diferença que realmente existe. Por exemplo, um cientista em uma empresa farmacêutica deve ter um alto grau de certeza sobre uma afirmação de que novo medicamento da empresa reduz significativamente os sintomas. O cientista escolhe um nível de significância de 0,001 para ter mais a certeza de que qualquer diferença significativa nos sintomas realmente exista.
N
O tamanho amostral (N) é o número total de observações na amostra.
Interpretação
O tamanho amostral afeta o poder do teste.
Normalmente, um tamanho amostral maior dá ao teste mais poder para detectar um outlier. Para obter mais informações, acesse O que é potência?.
Média
A média é a média dos dados, que é a soma de todas as observações divididas pelo número de observações.
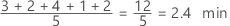
Interpretação
Use a média para descrever a amostra com um único valor que representa o centro dos dados. Diversas análises estatísticas usam a média como uma média padrão do centro da distribuição dos dados.
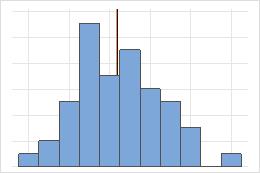
Simétrica
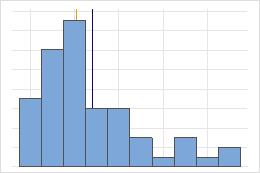
Não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são tão similares que você não pode ver facilmente as linhas. Mas a distribuição não simétrica é assimétrica à direita.
StDev
O desvio padrão é a medida mais comum de dispersão, ou o quanto os dados estão dispersos sobre a média. O símbolo σ (sigma) é frequentemente usado para representar o desvio padrão de uma população, enquanto s é usado para representar o desvio padrão de uma amostra. A variação que é aleatória ou natural de um processo é frequentemente referida como ruído.
Como o desvio padrão está nas mesmas unidades que os dados, ele é normalmente mais fácil de interpretar do que a variância.
Interpretação
Use o desvio padrão para determinar o grau de dispersão dos dados a partir da média. Um valor de desvio padrão mais alto indica maior dispersão nos dados. Uma boa regra de ouro de uma distribuição normal é que aproximadamente 68% dos valores estão dentro de um desvio padrão da média, 95% dos valores estão dentro de dois desvios padrão e 99,7% dos valores estão dentro de três desvios padrão.
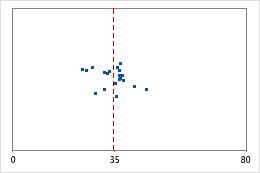
Hospital 1
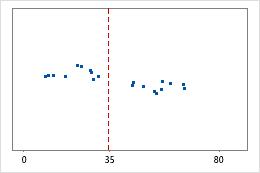
Hospital 2
Tempos de alta de hospital
Os administradores controlam o tempo gasto na alta de pacientes tratados nos departamentos de emergência de dois hospitais. Apesar de os tempos médios de alta serem quase os mesmos (35 minutos), os desvios padrão são significativamente diferentes. O desvio padrão do hospital 1 é de cerca de 6. Em média, o tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 6 minutos. O desvio padrão do hospital 2 é de cerca de 20. Na média, um tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 20 minutos.
Máximo
O valor máximo é o maior valor de dados.
Nesses dados, o máximo é 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o máximo para identificar um possível outlier ou um erro de entrada de dados. Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo. Se o valor máximo for muito elevado, mesmo quando se considerar o centro, a dispersão e o formato dos dados, investigue a causa do valor extremo.
Mínimo
O mínimo é o menor valor de dados.
Em nesses dados, o mínimo é 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o mínimo para identificar um possível outlier ou um erro de entrada de dados. Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo. Se o valor mínimo for muito baixo, mesmo quando se considerar o centro, a dispersão e o formato dos dados, investigue a causa do valor extremo.
Outlier
Um outlier é uma observação atipicamente grande ou pequeno. Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais).
Número da
A linha na worksheet que contém o outlier. O Minitab exibe este valor somente quando existe um outlier.
x[i] e x[N-i]
Quando você usa um dos testes de razão de Dixon, o Minitab exibe mais observações na tabela de teste, além de o mínimo e o máximo. O valor entre parênteses indica o tamanho da observação em relação aos outros valores. Por exemplo, x[2] indica a 2a menor observação e x[N-1] indica a 2a maior observação.
G
Teste estatístico de Grubbs (G) é a diferença entre a média da amostra e o maior ou menor valores de dados, dividido pelo desvio padrão. O Minitab usa a estatística de teste de Grubbs para calcular o valor de p, que é a probabilidade de rejeitar a hipótese nula quando ela é verdadeira.
P
O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor de p menor fornece uma evidência mais forte contra a hipótese nula.
Interpretação
Use o valor de p para determinar se existe um outlier.
- Valor de p ≤ α: Existe um outlier (rejeite H0)
- Se o valor de p é menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que existe um outlier. Tente identificar a causa de todos os outliers. Corrija quaisquer erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais).
- Valor de p > α: Não é possível concluir que existe um outlier (não deve rejeitar H0)
- Se o valor de p é maior do que o nível de significância, você não deve rejeitar a hipótese nula, porque não há evidências suficientes para concluir que existe um outlier. Você deve se certificar de que o teste tem poder suficiente para detectar um outlier. Para obter mais informações, acesse Aumentar a potência.
Gráfico de outlier
Um gráfico de outlier é semelhante a um gráfico individual. Use o gráfico de outlier para identificar visualmente um outlier nos dados. Se existir um outlier, o Minitab o representa no gráfico como um quadrado vermelho. Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais).
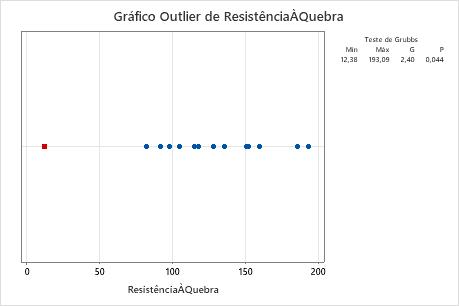
Nestes resultados, o menor valor, 12,38, é um outlier.
