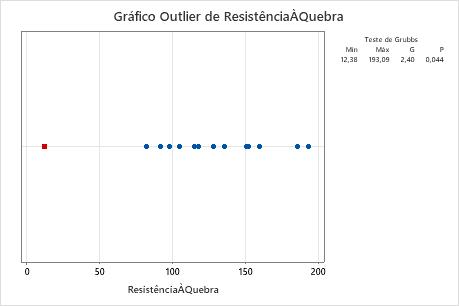
Um engenheiro de qualidade em uma empresa de cabos de madeira testa a resistência de uma amostra aleatória de cabos de vassoura. O engenheiro registra a força necessária para quebrar cada cabo. O engenheiro cria um gráfico dos dados e percebe que um dos valores na amostra parece extraordinariamente pequeno.
O engenheiro realiza um teste de outlier para determinar se o menor valor é um outlier.
- Abra os dados amostrais, ResistênciaDoCabo.MWX.
- Selecione .
- Em Variáveis, insira ResistênciaÀQuebra.
- Clique em Opções.
- Em O que você deseja determinar? (Hipótese alternativa), selecione O menor valor dos dados é um outlier.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
A média da amostra é 123,4. A estatística G indica que o menor valor dos dados, 12,38, é de 2,4 dos desvios padrão menor do que a média. O valor de p indica que, se todos os valores forem verdadeiramente a partir da mesma população distribuída normalmente, a probabilidade de obtenção de um valor mínimo, que seja pequeno é de apenas 0,044. Como o valor de p de 0,044 é menor do que o nível de significância (denotado como α ou alfa) de 0,05, o engenheiro rejeita a hipótese nula e conclui que o menor valor é um outlier.
O engenheiro investiga e descobre que a pessoa que inseriu os dados acidentalmente digitou 12,38 em vez de 123,8.
Método
| Hipótese nula | Todos os valores de dados são provenientes da mesma população normal |
|---|---|
| Hipótese alternativa | O menor valor dos dados é um outlier |
| Nível de significância | α = 0,05 |
Teste de Grubbs
| Variável | N | Média | DesvPad | Mín | Máx | G | P |
|---|---|---|---|---|---|---|---|
| ResistênciaÀQuebra | 14 | 123,4 | 46,3 | 12,4 | 193,1 | 2,40 | 0,044 |
Outlier
| Variável | Linha | Outlier |
|---|---|---|
| ResistênciaÀQuebra | 10 | 12,38 |