Neste tópico
Média
Uma medida tipicamente utilizada do centro de um grupo de números. A média é também chamada de a média. Ela é a soma de todas as observações dividida pelo número de observações (não faltantes).
Fórmula
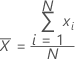
Notação
| Termo | Descrição |
|---|---|
| xi | ia observação |
| N | número de observações não ausentes |
Desvio padrão (StDev)
O desvio padrão da amostra fornece uma medida da dispersão dos seus dados. Ela é igual à raiz quadrada da variância da amostra.
Fórmula
, então, o desvio padrão dos dados da amostra é:
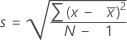
Notação
| Termo | Descrição |
|---|---|
| x i | i a observação |
 | média das observações |
| N | número de observações não ausentes |
N
Estatística de Anderson-Darling (A2)
A2 mede a área entre a linha ajustada (que se baseia na distribuição escolhido) e na função da etapa não-paramétrica (que tem por base os pontos do gráfico). A estatística é uma distância ao quadrado que é ponderado mais pesadamente nas caudas da distribuição. Um valor pequeno de Anderson-Darling indica que a distribuição se ajusta melhor aos dados.
O teste de normalidade de Anderson-Darling é definido como:
H0: os dados seguem uma distribuição normal.
H1: os dados não seguem uma distribuição normal.
Fórmula
Notação
| Termo | Descrição |
|---|---|
| F(Yi) |  , que é a função de distribuição acumulada da distribuição normal padrão |
| Yi | dados ordenados |
Ryan-Joiner
O teste de Ryan-Joiner fornece um coeficiente de correlação, o que indica a correlação entre os dados e as contagens normais de seus dados. Se o coeficiente de correlação estiver próximo de 1, seus dados ficarão próximos do gráfico de probabilidade normal. Se for menor que o valor crítico adequado, você vai rejeitar a hipótese nula de normalidade.
Fórmula
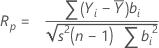
Notação
| Termo | Descrição |
|---|---|
| Yi | Observações ordenadas |
| bi | contagens normais de seus dados ordenados |
| s2 | variância da amostra |
Kolmogorov-Smirnov
Fórmula
- H0: Os dados seguem uma distribuição normal.
- H1: Os dados não seguem uma distribuição normal.
Notação
| Termo | Descrição |
|---|---|
| D+ | maxi {i / n – Z (i)} |
| D– | maxi {Z (i) – (i – 1) / n)} |
| Z | F(X(i)) |
| F(x) | função de distribuição de probabilidade da distribuição normal |
| X(i) | ia estatística de ordem de uma amostra aleatória, 1 ≤ i ≤ n |
| n | tamanho amostral |
Valor p
Outra medida quantitativa para informar o resultado do teste de normalidade é o valor de p. Um valor de p baixo é uma indicação de que a hipótese nula é falsa.
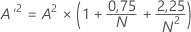
- Se 13 > A'2 > 0,600 então p = exp(1,2937 - 5,709 * A'2 + 0,0186(A'2)2)
- Se 0,600 > A'2 > 0,340 então p = exp(0,9177 - 4,279 * A'2 – 1,38(A'2)2)
- Se 0,340 > A'2 > 0,200 então p = 1 – exp(–8,318 + 42,796 * A'2 – 59,938(A'2)2)
- Se A'2 <0,200 então p = 1 – exp(–13,436 + 101,14 * A'2 – 223,73(A'2)2)
Pontos do gráfico
Em geral, quanto mais próximos estiverem os pontos da linha ajustada, melhor o ajuste. O Minitab fornece duas medidas de qualidade de ajuste para ajudar a avaliar a forma como a distribuição ajusta seus dados.
Fórmula
| Distribuição | coordenada x | coordenada y |
|---|---|---|
| Normal | x | Φ–1 norm |
Notação
| Termo | Descrição |
|---|---|
| Φ–1 norm | valor retornado para p pela fda inversa para a distribuição normal padrão |
Gráficos de probabilidade
Os dados de entrada estão representados graficamente como valores de x. O Minitab calcula a probabilidade de ocorrência sem supor uma distribuição. A escala Y no gráfico assemelha-se à escala Y encontrada no artigo sobre probabilidade normal, em que as probabilidades são representadas graficamente como uma linha reta, como se os dados fossem de uma distribuição normal.
