Média
A média descreve a amostra com um único valor que representa o centro dos dados. A média é calculada como a média dos dados, que é a soma de todas as observações divididas pelo número de observações.
N
O tamanho amostral (N) é o número total de observações na amostra.
Interpretação
O tamanho amostral afeta o poder do teste.
Normalmente, um tamanho amostral maior do teste dá mais poder para detectar uma diferença entre os dados de exemplo e a distribuição normal. Ou seja, quando uma diferença realmente existe, você tem uma chance maior de detectá-la com um tamanho amostral maior.
StDev
O desvio padrão é a medida mais comum de dispersão, ou quão dispersos os dados estão da média. A maior desvio padrão da amostra indica que os seus dados estão espalhados mais amplamente em torno da média.
AD
A estatística de qualidade de ajuste de Anderson-Darling (AD) mede a área entre a linha ajustada (com base na distribuição normal) e a função de distribuição empírica (que tem por base os pontos de dados). A estatística Anderson-Darling é uma distância ao quadrado que é ponderada mais pesadamente nas caudas da distribuição.
Interpretação
O Minitab usa a estatística de Anderson-Darling para calcular o valor de p. O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor de p menor fornece uma evidência mais forte contra a hipótese nula. Valores maiores para a estatística de Anderson-Darling indicam que os dados não seguem a distribuição normal.
KS
O teste de Kolmogorov-Smirnov compara o ECDF (função de distribuição acumulada empírica) de seus dados de amostra com a distribuição esperada se os dados foram normais.
Interpretação
O Minitab utiliza a estatística de Kolmogorov-Smirnov para calcular o valor de p. O valor de p é a probabilidade de se obter uma estatística de teste (como a estatística de Kolmogorov-Smirnov) que seja pelo menos tão extrema quanto o valor que é calculado a partir da amostra, quando os dados são normais. Valores maiores para a estatística de Kolmogorov-Smirnov indicam que os dados não seguem a distribuição normal.
RJ
A estatística de Ryan-Joiner mede o quão bem os dados seguem uma distribuição normal, calculando a correlação entre os dados e as contagens normais de seus dados. Se o coeficiente de correlação estiver próximo de 1, a população tende a ser normal. Este teste é semelhante ao teste de normalidade de Shapiro-Wilk.
Interpretação
O Minitab usa a estatística de Ryan-Joiner para calcular o valor de p. O valor de p é a probabilidade de se obter uma estatística de teste (como a estatística de Ryan-Joiner) que seja pelo menos tão extrema quanto o valor que é calculado a partir da amostra, quando os dados são normais. Valores maiores para a estatística de Ryan-Joiner indicam que os dados não seguem a distribuição normal.
Valor de p
O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor de p menor fornece uma evidência mais forte contra a hipótese nula.
Interpretação
Use o valor de p para determinar se os dados não seguem uma distribuição normal.
- Valor de p ≤ α: Os dados não seguem uma distribuição normal (Rejeite H0)
- Se o valor de p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os seus dados não seguem a distribuição normal.
- Valor de p > α: Não é possível concluir que os dados não seguem uma distribuição normal (não deve rejeitar H0)
- Se o valor de p for maior do que o nível de significância, você não deve rejeitar a hipótese nula. Não há evidências suficientes para concluir que os dados não seguem uma distribuição normal.
Gráfico de probabilidade
O gráfico de probabilidade cria uma função de distribuição acumulada estimada (FDA) a partir da sua amostra representando graficamente o valor de cada observação contra a probabilidade acumulada estimada da observação.
Interpretação
Use um gráfico de probabilidade para visualizar em que medida seus dados se ajustam bem à distribuição normal.
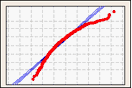
Dados assimétricos à direita
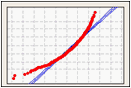
Dados assimétricos à esquerda
Dica
No Minitab, mantenha o cursor sobre a linha de distribuição ajustada para ver um gráfico de percentis e valores.
