Neste tópico
Estatística de Anderson-Darling (A2)
A2 mede a área entre a linha ajustada (que se baseia na distribuição escolhido) e na função da etapa não-paramétrica (que tem por base os pontos do gráfico). A estatística é uma distância ao quadrado que é ponderado mais pesadamente nas caudas da distribuição. Um valor pequeno de Anderson-Darling indica que a distribuição se ajusta melhor aos dados.
O teste de normalidade de Anderson-Darling é definido como:
H0: os dados seguem uma distribuição normal.
H1: os dados não seguem uma distribuição normal.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| F(Yi) |  , que é a função de distribuição acumulada da distribuição normal padrão , que é a função de distribuição acumulada da distribuição normal padrão |
| Yi | dados ordenados |
Valor de P para o teste de normalidade de Anderson-Darling
A medida quantitativa para relatar o resultado do teste de normalidade de Anderson-Darling é o valor de p. Um valor de p pequeno indica que a hipótese nula é falsa.
Se você conhecer A2 poderá calcular o valor de p.
Permita que
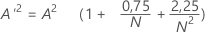
- Se 13 > A'2 > 0,60 então p = exp(1,2937 - 5,709 * A'2 + 0,0186(A'2)2)
- Se 0,60 > A'2 > 0,34 então p = exp(0,9177 - 4,279 * A'2 – 1,38(A'2)2)
- Se 0,34 > A'2 > 0,20 então p = 1 – exp(–8,318 + 42,796 * A'2 – 59,938(A'2)2)
- Se A'2 < 0,200 então p = 1 – exp(–13,436 + 101,14 * A'2 – 223,73(A'2)2)
N não faltantes (N)
O número de valores não faltantes na amostra.
Desvio padrão (StDev)
O desvio padrão da amostra fornece uma medida da dispersão dos seus dados. Ela é igual à raiz quadrada da variância da amostra.
Fórmula
 , então, o desvio padrão dos dados da amostra é:
, então, o desvio padrão dos dados da amostra é:
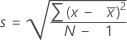
Notação
| Termo | Descrição |
|---|---|
| x i | i a observação |
 | média das observações |
| N | número de observações não ausentes |
Variância
A variância mede o quanto os dados estão dispersos em relação à sua média. A variância é igual ao desvio padrão ao quadrado.
Fórmula
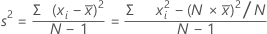
Notação
| Termo | Descrição |
|---|---|
| xi | ia observação |
 | média das observações |
| N | número de observações não ausentes |
Assimetria
A assimetria é uma medida de assimetria. Um valor negativo indica assimetria para a esquerda e um valor positivo indica assimetria para a direita. Um valor zero não indica necessariamente simetria.
Fórmula
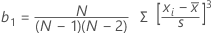
Notação
| Termo | Descrição |
|---|---|
| xi | i a observação |
 | média das observações |
| N | número de observações não ausentes |
| s | desvio padrão da amostra |
Curtose
Curtose é uma medida de quantidade de diferença de uma distribuição a partir da distribuição normal. Um valor positivo geralmente indica que a distribuição tem um pico mais acentuado do que a distribuição normal. Um valor negativo indica que a distribuição tem um pico mais plano do que a distribuição normal.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| xi | i a observação |
 | média das observações |
| N | número de observações não ausentes |
| s | desvio padrão da amostra |
Média
Uma medida tipicamente utilizada do centro de um grupo de números. A média é também chamada de a média. Ela é a soma de todas as observações dividida pelo número de observações (não faltantes).
Fórmula
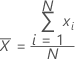
Notação
| Termo | Descrição |
|---|---|
| xi | ia observação |
| N | número de observações não ausentes |
Mínimo
O menor valor em seu conjunto de dados.
Máximo
O maior valor em seu conjunto de dados.
1o quartil (Q1)
25% das suas observações da amostra são menores ou iguais ao valor do 1o quartil. Portanto o 1o quartil também é conhecido como o 25o percentil.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| y | valor inteiro truncado de w |
| w | 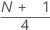 |
| z | componente fracionário de w que foi truncado |
| xj | ja observação na lista de dados da amostra, ordenada do menor ao maior |
Observação
Quando w é um inteiro, y = w, z = 0 e Q1 = xy.
Mediana
A mediana da amostra fica no meio dos dados: pelo menos metade das observações são menores ou iguais a ela, e pelo menos metade são maiores ou iguais a ela.
Suponha que você tenha uma coluna que contém valores de N. Para calcular a mediana, primeiro ordene seus valores de dados do menor ao maior. Se N for ímpar, a mediana da amostra é o valor no meio. Se N for par, a mediana da amostra é a média dos dois valores do meio.
Por exemplo, quando N = 5 e você tem dados x1, x2, x3, x4 e x5, a mediana = x3.
Quando N = 6 e você ordenou os dados x1, x2, x3, x4, x5 e x6:

em que x3 e x4 são a terceira e quarta observações.
3o. quartil (Q3)
75% das suas observações da amostra são menores ou iguais ao valor do terceiro quartil. Portanto, o terceiro quartil também é conhecido como o 75o percentil.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| y | valor truncado de w |
| w |
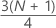 |
| z | componente fracionário de w que foi truncado |
| xj | ja observação na lista de dados da amostra, ordenada do menor ao maior |
Observação
Quando w é um inteiro, y = w, z = 0 e Q3 = xy.
Intervalo de confiança para a média
Fórmula

Notação
| Termo | Descrição |
|---|---|
 | média |
| s | desvio padrão da amostra |
| N | número não faltante |
| t N, α | probabilidade acumulada inversa de uma distribuição t com n-1 graus de liberdade em 1-α/2; α = 1 – nível de confiança / 100 |
Intervalo de confiança para a mediana
O Minitab usa interpolação linear para calcular o intervalo de confiança para a média verdadeira 1. Este método é uma aproximação muito boa para uma grande variedade de distribuições simétricas, incluindo a distribuição normal, a distribuição de Cauchy, e a distribuição uniforme. Exemplos de distribuições não simétricas mostram resultados adequados que são sempre muito mais preciso do que a interpolação linear.
Intervalo de confiança para o desvio padrão
O Minitab calcula um intervalo de confiança de (1 – α) 100% para o desvio padrão da população, σ. O intervalo de confiança é muito sensível à suposição de que os dados são normais. Mesmo pequenos desvios da normalidade podem resultar em um intervalo de confiança equivocado.
Fórmula
O intervalo de confiança vai de:
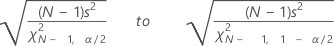
Notação
| Termo | Descrição |
|---|---|
| s | desvio padrão |
| N | número não faltante |
| χ2N, α | probabilidade acumulada inversa de um χ2 com N graus de liberdade a 1 – α / 2; α = 1 – nível de confiança / 100 |
