Neste tópico
Etapa 1: Descreva o centro de seus dados
Use a média para descrever a amostra com um único valor que representa o centro dos dados. Diversas análises estatísticas usam a média como uma média padrão do centro da distribuição dos dados.
A mediana é outra medida do centro da distribuição dos dados. A mediana é normalmente menos influenciada por outliers do que a média. Metade dos valores dos dados são maiores do que o valor da mediana e metade dos valores dos dados são menores do que o valor da mediana.
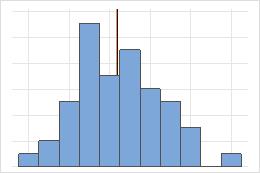
Simétrica
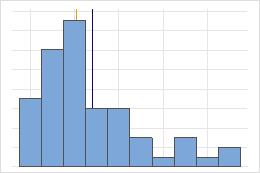
Não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são tão similares que você não pode ver facilmente as linhas. Mas a distribuição não simétrica é assimétrica à direita.
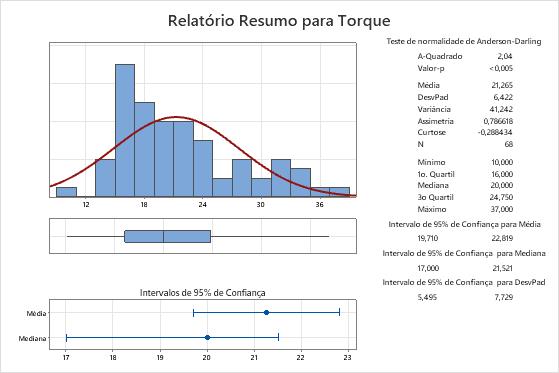
Principais resultados: média e mediana
Nesses resultados, o torque médio necessário para remover a tampa do creme dental é 21,265, e o torque mediano é 20. Os dados parecem estar assimétricos à direita, o que explica a razão pela qual a média é maior do que a mediana.
Etapa 2: Determine um intervalo de confiança para a média, mediana e desvio padrão
O intervalo de confiança fornece um intervalo de valores possíveis para o parâmetro da população. Por exemplo, um nível de confiança de 95% indica que, se você extrair 100 amostras aleatórias da população, poderia esperar que, aproximadamente, 95 das amostras produza intervalos que contêm o parâmetro da população.

Principais resultados: Intervalo de Confiança para Média, intervalo de Confiança para Mediana, Intervalo de confiança para StDev
- A média da população para as medições de torque está entre 19,710 e 22.819.
- A mediana da população para as medições de torque está entre 17 e 21,521.
- O desvio padrão da população para as medições de torque está entre 5,495 e 7,729.
Passo 3: Avalie a forma e a dispersão de sua distribuição de dados
Utilizar o histograma e boxplot para avaliar a forma e a dispersão dos dados e identificar os outliers potenciais.
Examinar a dispersão de seus dados para determinar se eles parecem ser assimétricos
Quando os dados são assimétricos, a maioria dos dados está localizada no lado alto ou baixo do gráfico. Muitas vezes, é mais fácil detectar a assimetria com um histograma ou boxplot.
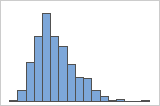
Assimétrico à direita
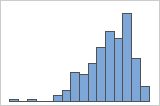
Assimétrico à esquerda
O histograma com dados assimétricos à direita mostra os tempos de espera. A maioria dos tempos de espera são relativamente curtos e apenas alguns tempos de espera são longos. O histograma com dados assimétricos à esquerda mostram dados de tempo de falha. Alguns itens falham imediatamente e muitos outros itens falham posteriormente.
Identificar outliers
Outliers, que são valores de dados que estão distantes de outros valores de dados, podem afetar fortemente os resultados de sua análise. Muitas vezes, os outliers são mais fáceis de serem identificados em um boxplot.
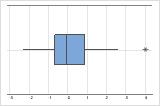
Em um boxplot, asteriscos (*) denotam outliers.
Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais). Depois, repita a análise. Para obter mais informações, acesse Identificação de outliers.
Procurar por dados multimodais
Os dados multimodais têm vários picos, também chamados de modos. Os dados multimodais, muitas vezes, indicam que variáveis importantes ainda não foram contabilizadas.
Se você tiver informações adicionais que lhe permitam classificar as observações em grupos, pode criar uma variável de grupo com estas informações. Em seguida, pode criar o gráfico com grupos para determinar se a variável de grupo representa os picos nos dados.
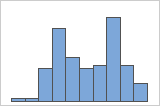
Simples
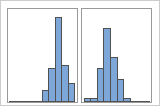
Com grupos
Por exemplo, um gerente de um banco coleta os dados de tempo de espera e cria um histograma simples. O histograma parece ter dois picos. Após uma investigação mais aprofundada, o gerente determina que os tempos de espera para os clientes que estão descontando cheques é menor do que os tempos de espera para os clientes que estão se candidatando a empréstimos imobiliários. O gerente acrescenta uma variável de grupo para a tarefa do cliente e, em seguida, cria um histograma com grupos.
