Neste tópico
A ao quadrado
A estatística de qualidade de ajuste de Anderson-Darling (A ao quadrado) mede a área entre a linha ajustada (com base na distribuição normal) e a função de distribuição empírica (que tem por base os pontos de dados). A estatística Anderson-Darling é uma distância ao quadrado que é ponderada mais pesadamente nas caudas da distribuição.
Interpretação
O Minitab usa a estatística de Anderson-Darling para calcular o valor de p. O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor de p menor fornece uma evidência mais forte contra a hipótese nula. Um valor menor para a estatística Anderson-Darling indica que os dados seguem a distribuição normal mais de perto.
Valor de p
O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor de p menor fornece uma evidência mais forte contra a hipótese nula.
Interpretação
Use o valor de p para determinar se os dados não seguem uma distribuição normal.
- Valor de p ≤ α: Os dados não seguem uma distribuição normal (Rejeite H0)
- Se o valor de p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os seus dados não seguem a distribuição normal.
- Valor de p > α: Não é possível concluir que os dados não seguem uma distribuição normal (não deve rejeitar H0)
- Se o valor de p for maior do que o nível de significância, você não deve rejeitar a hipótese nula. Não há evidências suficientes para concluir que os dados não seguem uma distribuição normal.
Média
A média é a média dos dados, que é a soma de todas as observações divididas pelo número de observações.
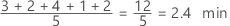
Interpretação
Use a média para descrever a amostra com um único valor que representa o centro dos dados. Diversas análises estatísticas usam a média como uma média padrão do centro da distribuição dos dados.
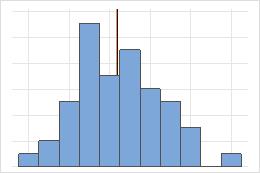
Simétrica
Não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são tão similares que você não pode ver facilmente as linhas. Mas a distribuição não simétrica é assimétrica à direita.
StDev
O desvio padrão é a medida mais comum de dispersão, ou o quanto os dados estão dispersos sobre a média. O símbolo σ (sigma) é frequentemente usado para representar o desvio padrão de uma população, enquanto s é usado para representar o desvio padrão de uma amostra. A variação que é aleatória ou natural de um processo é frequentemente referida como ruído.
Como o desvio padrão está nas mesmas unidades que os dados, ele é normalmente mais fácil de interpretar do que a variância.
Interpretação
Use o desvio padrão para determinar o grau de dispersão dos dados a partir da média. Um valor de desvio padrão mais alto indica maior dispersão nos dados. Uma boa regra de ouro de uma distribuição normal é que aproximadamente 68% dos valores estão dentro de um desvio padrão da média, 95% dos valores estão dentro de dois desvios padrão e 99,7% dos valores estão dentro de três desvios padrão.
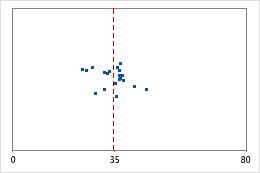
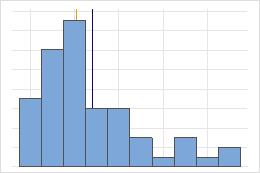
Hospital 1
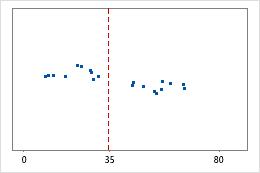
Hospital 2
Tempos de alta de hospital
Os administradores controlam o tempo gasto na alta de pacientes tratados nos departamentos de emergência de dois hospitais. Apesar de os tempos médios de alta serem quase os mesmos (35 minutos), os desvios padrão são significativamente diferentes. O desvio padrão do hospital 1 é de cerca de 6. Em média, o tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 6 minutos. O desvio padrão do hospital 2 é de cerca de 20. Na média, um tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 20 minutos.
Variância
A variância mede o quanto os dados estão dispersos em relação à sua média. A variância é igual ao desvio padrão ao quadrado.
Interpretação
Quanto maior a variância, maior a dispersão nos dados.
Como a variância (σ2) é uma quantidade quadrada, suas unidades também são quadradas, o que torna a variância difícil de usar, na prática. O desvio padrão é normalmente mais fácil de interpretar porque ele está nas mesmas unidades que os dados. Por exemplo, uma amostra de tempos de espera em uma parada de ônibus pode ter uma média de 9 minutos2. Como a variância não está nas mesmas unidades que os dados, com frequência, ela é exibida com sua raiz quadrada, o desvio padrão. Uma variância de 9 minutos2 é equivalente a um desvio padrão de 3 minutos.
Assimetria
A assimetria é a medida em que os dados não são simétricos.
Interpretação
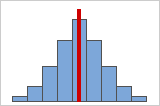
Figura A
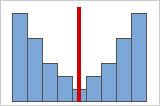
Figura B
Distribuições simétricas ou não assimétricas
Conforme os dados tornam-se simétricos, seu valor de assimetria aproxima-se de zero. A Figura A mostra dados de distribuição normal, que por definição exibe assimetria relativamente pequena. Ao traçar uma linha abaixo do meio deste histograma de dados normais é fácil de ver que os dois lados refletem um ao outro. Mas a falta de assimetria simplesmente não significa normalidade. A Figura B mostra uma distribuição onde os dois lados ainda refletem um ao outro, apesar de os dados estarem longe de serem uma distribuição normal.
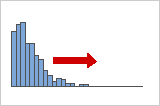
Distribuições com assimetria positiva ou à direita
Dados com assimetria positiva ou à direita são assim chamados por causa da "cauda" dos pontos de distribuição à direita, e porque seu valor de assimetria será maior do que 0 (ou positiva). Dados salariais são, frequentemente, assimétricos desta maneira: vários funcionários em uma empresa ganham relativamente pouco, enquanto cada vez menos pessoas ganham altos salários.
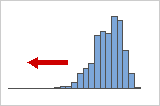
Distribuições com assimetria negativa ou à esquerda
Assimetria à esquerda ou dados assimétricos negativos são assim chamados porque a "cauda" da distribuição aponta para a esquerda, e porque ela produz um valor de assimetria negativo. Os dados da taxa de falha são frequentemente assimétricos à esquerda. Considere as lâmpadas: muito poucas vão queimar imediatamente, a grande maioria durará por um longo tempo.
Curtose
A curtose indica como as caudas de uma distribuição diferem da distribuição normal.
Interpretação
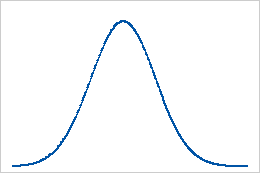
Linha de base: valor da curtose de 0
Normalmente os dados distribuídos estabelecem a linha de base para a curtose. Um valor de curtose de 0 indica que os dados seguem a distribuição normal perfeitamente. O valor da curtose que se desvia significativamente de 0 pode indicar que os dados não estão normalmente distribuídos.
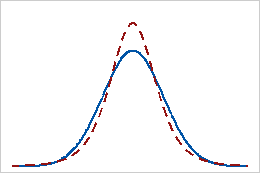
Curtose positiva
Uma distribuição com um valor de curtose positiva indica que a distribuição tem caudas mais pesadas do que a distribuição normal. Por exemplo, os dados que se seguem à distribuição T têm um valor de curtose positivo. A linha contínua mostra a distribuição normal e a linha pontilhada mostra uma distribuição com um valor de curtose positivo.
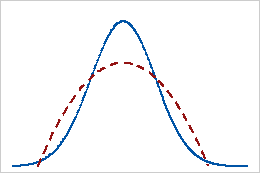
Curtose negativa
Uma distribuição com um valor de curtose negativa indica que a distribuição tem caudas mais leves do que a distribuição normal. Por exemplo, os dados que seguem uma distribuição beta com primeiro e segundo parâmetros de forma igual a 2 têm um valor de curtose negativo. A linha contínua mostra a distribuição normal e a linha pontilhada mostra uma distribuição com um valor de curtose negativo.
N
O número de valores não faltantes na amostra.
| Contagem total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Mínimo
O mínimo é o menor valor de dados.
Em nesses dados, o mínimo é 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o mínimo para identificar um possível outlier ou um erro de entrada de dados. Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo. Se o valor mínimo for muito baixo, mesmo quando se considerar o centro, a dispersão e o formato dos dados, investigue a causa do valor extremo.
1o. quartil
Quartis são os três valores — o 1o quartil a 25% (Q1), o segundo quartil a 50% (Q2 ou mediana) e o terceiro quartil a 75% (Q3)— que dividem uma amostra de dados ordenados em quatro partes iguais.
O 1o quartil o 25o percentil e indica que 25% dos dados são menores ou iguais a este valor.
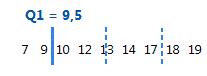
Para estes dados ordenados, o 1o quartil (Q1) é 9,5. Ou seja, 25% dos dados são menores ou iguais a 9,5.
Mediana
A mediana é o ponto médio do conjunto de dados. Este valor do ponto médio é o ponto em que metade das observações estão acima do valor e metade das observações estão abaixo do valor. A mediana é determinada por classificar as observações e encontrar a observação que está no número [N + 1] / 2 na ordem de grandeza. Se o número de observações for ímpar, a mediana é o valor médio das observações que são classificadas com números de N / 2 e [N / 2] + 1.
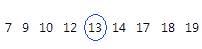
Para esses dados ordenados, a mediana é 13. Isto é, metade dos valores é menor ou igual a 13, e metade dos valores é maior ou igual a 13. Se você adicionar outra observação igual a 20, a mediana será 13,5, que é a média entre a 5a observação (13) e a 6a observação (14).
Interpretação

Simétrica

Não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são tão similares que você não pode ver facilmente as linhas. Mas a distribuição não simétrica é assimétrica à direita.
3o. quartil
Quartis são os três valores — o 1o quartil a 25% (Q1), o segundo quartil a 50% (Q2 ou mediana) e o terceiro quartil a 75% (Q3)— que dividem uma amostra de dados ordenados em quatro partes iguais.
O terceiro quartil é o 75o percentil e indica que 75% dos dados são menores ou iguais a este valor.
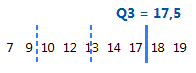
Para estes dados ordenados, o terceiro quartil (Q3) é 17,5. Ou seja, 75% dos dados são menores ou iguais a 17,5.
Máximo
O valor máximo é o maior valor de dados.
Nesses dados, o máximo é 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o máximo para identificar um possível outlier ou um erro de entrada de dados. Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo. Se o valor máximo for muito elevado, mesmo quando se considerar o centro, a dispersão e o formato dos dados, investigue a causa do valor extremo.
Intervalo de Confiança
O intervalo de confiança fornece um intervalo de valores possíveis para o parâmetro da população. Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. Porém, se você repetir sua amostra muitas vezes, uma certa porcentagem dos intervalos ou fronteiras de confiança resultantes contém o parâmetro de população desconhecida. A porcentagem destes intervalos de confiança ou fronteiras que contêm o parâmetro é o nível de confiança do intervalo. Por exemplo, um nível de confiança de 95% indica que, se você extrair 100 amostras aleatórias da população, poderia esperar que, aproximadamente, 95 das amostras produza intervalos que contêm o parâmetro da população.
Um limite superior define um valor provável que o parâmetro da população seja menor. Um limite inferior define um valor provável que o parâmetro da população seja maior.
O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra. Para obter mais informações, vá para Como obter um intervalo de confiança mais preciso.
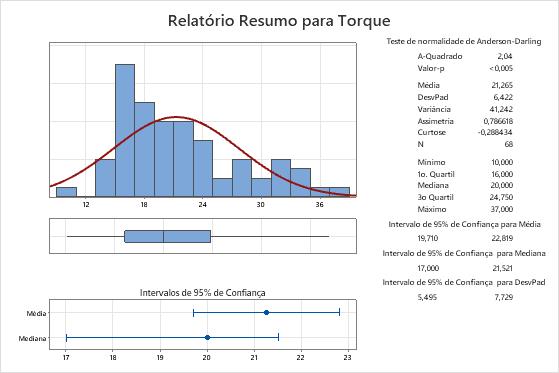
- A média da população para as medições de torque está entre 19,710 e 22.819.
- A mediana da população para as medições de torque está entre 17 e 21,521.
- O desvio padrão da população para as medições de torque está entre 5,495 e 7,729.
Histograma
Um histograma divide valores de amostra para muitos intervalos e representa a frequência de valores de dados em cada intervalo com uma barra.
Interpretação
Utilize um histograma para avaliar a forma e a dispersão dos dados. Os histogramas são melhores quando o tamanho amostral for superior a 20.
- Dados Assimétricos
-
Você pode usar um histograma dos dados sobrepostos por uma curva normal para analisar a normalidade de seus dados. Uma distribuição normal é simétrica e em forma de sino, como indicada pela curva. Muitas vezes, é difícil de avaliar a normalidade com amostras pequenas. É melhor usar um gráfico de probabilidade para determinar o ajuste de distribuição.
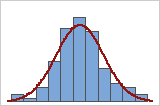
Bom ajuste
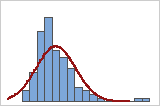
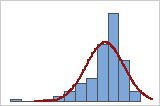
Ajuste ruim
- Outliers
-
Outliers, que são valores de dados que estão distantes de outros valores de dados, podem afetar fortemente os resultados de sua análise. Muitas vezes, os outliers são mais fáceis de serem identificados em um boxplot.
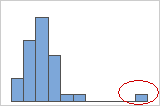
Em um histograma, barras isoladas em ambas as extremidades do gráfico identificam possíveis outliers.
Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais). Depois, repita a análise. Para obter mais informações, acesse Identificação de outliers.
- Dados multimodais
-
Os dados multimodais têm vários picos, também chamados de modos. Os dados multimodais, muitas vezes, indicam que variáveis importantes ainda não foram contabilizadas.
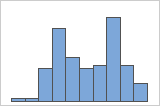
Simples
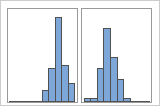
Com grupos
Por exemplo, um gerente de um banco coleta os dados de tempo de espera e cria um histograma simples. O histograma parece ter dois picos. Após uma investigação mais aprofundada, o gerente determina que os tempos de espera para os clientes que estão descontando cheques é menor do que os tempos de espera para os clientes que estão se candidatando a empréstimos imobiliários. O gerente acrescenta uma variável de grupo para a tarefa do cliente e, em seguida, cria um histograma com grupos.
Se você tiver informações adicionais que lhe permitam classificar as observações em grupos, pode criar uma variável de grupo com estas informações. Em seguida, pode criar o gráfico com grupos para determinar se a variável de grupo representa os picos nos dados.
Boxplot
Um boxplot fornece um resumo gráfico da distribuição de uma amostra. O boxplot mostra a forma, a tendência central e a variabilidade dos dados.
Interpretação
Utilize um boxplot para examinar a dispersão dos dados e identificar todos os outliers potenciais. Os boxplots são melhores quando o tamanho amostral for superior a 20.
- Dados Assimétricos
-
Examine a dispersão de seus dados para determinar se eles parecem ser assimétricos. Quando os dados são assimétricos, a maioria dos dados está localizada no lado alto ou baixo do gráfico. Muitas vezes, é mais fácil detectar a assimetria com um histograma ou boxplot.
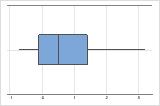
Assimétrico à direita
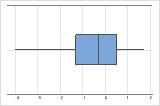
Assimétrico à esquerda
O boxplot com dados assimétricos à direita mostra os tempos de espera. A maioria dos tempos de espera são relativamente curtos e apenas alguns tempos de espera são longos. O boxplot com dados assimétricos à esquerda mostram dados de tempo de falha. Alguns itens falham imediatamente e muitos outros itens falham posteriormente.
- Outliers
-
Outliers, que são valores de dados que estão distantes de outros valores de dados, podem afetar fortemente os resultados de sua análise. Muitas vezes, os outliers são mais fáceis de serem identificados em um boxplot.
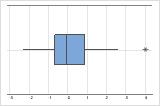
Em um boxplot, asteriscos (*) denotam outliers.
Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais). Depois, repita a análise. Para obter mais informações, acesse Identificação de outliers.
