Neste tópico
Média estimada
Fórmula
A média para a distribuição de Poisson é estimada como:
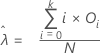
Cálculo
| Dados | 2 2 3 3 2 4 4 2 1 1 1 4 4 3 0 4 3 2 3 3 4 1 3 1 4 3 2 2 1 2 0 2 3 2 3 |
| Categoria (i) | Observado (Oi) | Média estimada | Probabilidade de Poisson (pi) |
|---|---|---|---|
| 0 | 2 | 0 * 2 = 0 | p0 = e-2.4 = 0.090718 |
| 1 | 6 | 1 * 6 = 6 | p1 = e-2.4 * 2.4 = 0.217723 |
| 2 | 10 | 2 * 10 = 20 | p2 = e-2.4 * (2.4)2/ 2! = 0.261268 |
| 3 | 10 | 3 * 10 = 30 | p3 = e-2.4 * (2.4)3/ 3! = 0.209014 |
 |
7 | 4 * 7 = 28 | p4 = 1 - (p0 + p1 +p2 + p3) = 0.221267 |
N = 35
Σ (i * Oi) = 84
Média estimada = 
Notação
| Termo | Descrição |
|---|---|
| N | soma de todos os valores observados (O0 + O1 + ...+ Ok) |
| k | (o número de categorias ) - 1 |
| Oi | o número observado de eventos na ia categoria |
| pi | Probabilidade de Poisson |
Número de categorias
O Minitab determina as categorias utilizando os métodos iterativos a seguir:
Definindo a primeira categoria
Permita que pi = P(X  xi )
xi )
Permita que i = 1: if N*pi  2, então, a primeira categoria é definida como "
2, então, a primeira categoria é definida como " x 1". If N*pi < 2, então, aumente i em um e repita: se N*p 2
x 1". If N*pi < 2, então, aumente i em um e repita: se N*p 2  2, então, a primeira categoria é definida como "
2, então, a primeira categoria é definida como " x 2". If N*pi < 2, aumente i em um e repita até N*pi
x 2". If N*pi < 2, aumente i em um e repita até N*pi  2. Pare as iterações quando esta condição for satisfeita primeiro, ou quando xi for o terceiro maior valor de dados e defina a primeira categoria como "
2. Pare as iterações quando esta condição for satisfeita primeiro, ou quando xi for o terceiro maior valor de dados e defina a primeira categoria como " xi ". Se o valor da primeira categoria for zero, a primeira categoria é definida como "0" sem o sinal "menor que" ou "igual a". O valor de probabilidade e o valor esperado associados à primeira categoria são pi e N*pi respectivamente. O valor observado para a primeira categoria é o número de todos os valores de dados
xi ". Se o valor da primeira categoria for zero, a primeira categoria é definida como "0" sem o sinal "menor que" ou "igual a". O valor de probabilidade e o valor esperado associados à primeira categoria são pi e N*pi respectivamente. O valor observado para a primeira categoria é o número de todos os valores de dados  xi .
xi .
Definindo a última categoria
Conceitualmente, definir a última categoria é semelhante a definir a primeira categoria, mas o Minitab funciona ao contrário, começando a partir do maior valor de dados.
A última categoria é " xj ", em que xj é o maior valor de dados maior do que (1 + o valor dos dados da primeira categoria), de modo que a categoria tem um valor esperado maior que 2. A probabilidade e o valor esperado para a última categoria são pj e N*pj respectivamente, e o valor observado é o número de valores de dados
xj ", em que xj é o maior valor de dados maior do que (1 + o valor dos dados da primeira categoria), de modo que a categoria tem um valor esperado maior que 2. A probabilidade e o valor esperado para a última categoria são pj e N*pj respectivamente, e o valor observado é o número de valores de dados  xj .
xj .
Definição das categorias intermediárias
Depois de determinar a primeira e a última categoria, o Minitab determina as categorias entre eles. Permita que "X  k" seja a primeira categoria, e "X
k" seja a primeira categoria, e "X  m" seja a última categoria. Se todos os inteiros entre (k, m) tiverem os valores esperados
m" seja a última categoria. Se todos os inteiros entre (k, m) tiverem os valores esperados  2, todos eles constituem uma categoria intermediária. Caso contrário, o Minitab usa um loop recursivo para agrupar múltiplos inteiros adjacentes em categorias com valores esperados
2, todos eles constituem uma categoria intermediária. Caso contrário, o Minitab usa um loop recursivo para agrupar múltiplos inteiros adjacentes em categorias com valores esperados  2. Há determinadas situações, como um conjunto de dados com algumas observações, em que o valor esperado de uma categoria será menor do que 2.
2. Há determinadas situações, como um conjunto de dados com algumas observações, em que o valor esperado de uma categoria será menor do que 2.
Notação
| Termo | Descrição |
|---|---|
| N | o número de observações total |
| xi | o i o valor no conjunto de dados após a ordenação do menor para o maior |
| pi | Probabilidade de Poisson |
Probabilidade de Poisson
Fórmula
A probabilidade de Poisson da i a categoria (i < k) é,

A probabilidade de Poisson para a última categoria, em que i = k,
pi = 1 – (p0 + p1 + ...+ pk-1)
Notação
| Termo | Descrição |
|---|---|
| k | o número de categorias |
| λ | a média estimada de sua amostra |
Número esperado
Fórmula
O número esperado de observações na i a categoria é N * pi .
Notação
| Termo | Descrição |
|---|---|
| N | tamanho amostral |
| pi | a probabilidade de Poisson associada à i a categoria |
Contribuição ao qui-quadrado
Fórmula
Contribuição da Ia categoria ao valor de qui-quadrado é calculada como
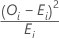
Notação
| Termo | Descrição |
|---|---|
| OI | o número observado de observações na Ia categoria |
| EI | o número esperado de observações na Ia categoria |
Estatística de teste
Fórmula
O teste qui-quadrado de qualidade de ajuste é calculado como,
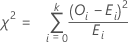
Notação
| Termo | Descrição |
|---|---|
| k | (o número de categorias ) - 1 |
| Oi | o número observado de observações na Ia categoria |
| Ei | o número esperado de observações na Ia categoria |
Valor de p e graus de liberdade
O valor de p é:
Prob (X > estatística de teste)
em que X segue uma distribuição qui-quadrado com k - 1 graus de liberdade se você usar o subcomando MEAN, ou k- 2 graus de liberdade se você não usar o subcomando MEAN.
Cálculo
| Dados | 2 2 3 3 2 4 4 2 1 1 1 4 4 3 0 4 3 2 3 3 4 1 3 1 4 3 2 2 1 2 0 2 3 2 3 |
| Categoria (i) | Observado (Oi) | Média estimada | Probabilidade de Poisson (pi) |
|---|---|---|---|
| 0 | 2 | 0 * 2 = 0 | p0 = e -2.4 = 0.090718 |
| 1 | 6 | 1 * 6 = 6 | p1 = e -2.4 * 2.4 = 0.217723 |
| 2 | 10 | 2 * 10 = 20 | p2 = e -2.4 * (2.4)2/ 2! = 0.261268 |
| 3 | 10 | 3 * 10 = 30 | p3 = e -2.4 * (2.4)3/ 3! = 0.209014 |
 |
7 | 4 * 7 = 28 | p4 = 1 - (p0 + p1 +p2 + p3 ) = 0.221267 |
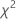 = ( 0,43492 + 0,344527 + 0,080058 + 0,985114 + 0,071545) = 1,91622
= ( 0,43492 + 0,344527 + 0,080058 + 0,985114 + 0,071545) = 1,91622
k = 5= o número de categorias
DF = 5- 2 = 3
valor de p = P (X > 1.91622) = 0.590
Notação
| Termo | Descrição |
|---|---|
| k | the number of categories |
| Oi | o número observado de observações na Ia categoria. |
| Ei | o número esperado de observações na Ia categoria. |
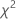 | estatística de teste qui-quadrado de qualidade de ajuste |
| DF | graus de liberdade |
