Neste tópico
Etapa 1: Determine se os dados não seguem uma distribuição de Poisson
- Valor de p ≤ α: Os dados não seguem uma distribuição de Poisson (Rejeite H0)
- Se o valor de p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os seus dados não seguem a distribuição de Poisson.
- Valor de p > α: Não é possível concluir que os dados não seguem uma distribuição de Poisson (não deve rejeitar H0)
- Se o valor de p é maior do que o nível de significância, você não deve rejeitar a hipótese nula, porque não há provas suficientes para concluir que os seus dados não seguem uma distribuição de Poisson.
Método
| Frequências em Observado |
|---|
Estatísticas Descritivas
| N | Média |
|---|---|
| 300 | 0,536667 |
Contagens observadas e esperadas para Defeitos
| Defeitos | Probabilidade de Poisson | Contagem observada | Contagem esperada | Contribuição para Qui-Quadrado |
|---|---|---|---|---|
| 0 | 0,584694 | 213 | 175,408 | 8,056 |
| 1 | 0,313786 | 41 | 94,136 | 29,993 |
| 2 | 0,084199 | 18 | 25,260 | 2,086 |
| >=3 | 0,017321 | 28 | 5,196 | 100,072 |
Teste qui-quadrado
| Hipótese nula | H₀: dados seguem uma distribuição de Poisson |
|---|---|
| Hipótese alternativa | H₁: dados não seguem uma distribuição de Poisson |
| GL | Qui-Quadrado | Valor-p |
|---|---|---|
| 2 | 140,208 | 0,000 |
Resultados principais: valor de p
Nestes resultados, a hipótese nula afirma que os dados seguem uma distribuição de Poisson. Como o valor de p é 0,000, que é inferior a 0,05, a decisão é rejeitar a hipótese nula. É possível concluir que os dados não vêm de uma distribuição de Poisson.
Etapa 2: Examine a diferença entre os valores observados e esperados para cada categoria
Use um gráfico de barras dos valores observados e esperados para determinar se, para cada categoria, o número de valores observados é diferente do número de valores esperados. As diferenças maiores entre os valores observados e esperados indicam que os dados não seguem uma distribuição de Poisson.
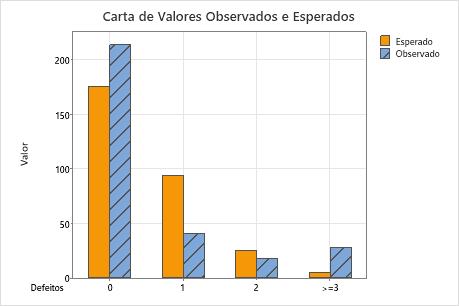
Este gráfico de barras indica que os valores observados para 0 defeitos, 1 defeito, e mais de 3 defeitos são diferentes dos valores esperados. Assim, o gráfico de barras confirma visualmente o que o valor de p indica, que é que os dados não seguem uma distribuição de Poisson.
