Neste tópico
Média
A média de Poisson é a soma de cada categoria multiplicada pelo número de valores observados naquela categoria, divididos pelo número total de valores observados.
N
O número de valores não faltantes na amostra.
| Contagem total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N*
Número de valores faltantes na amostra. O número de valores faltantes se refere às células que contêm o símbolo de valor faltante *.
| Contagem total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Probabilidade de Poisson
A probabilidade de cada categoria, assumindo que os dados seguem uma distribuição de Poisson que tem uma média que é igual à média de Poisson que é calculada a partir dos dados. O Minitab usa a probabilidade de Poisson para calcular os valores esperados.
Valores observados e esperados
Os valores observados são o número real de observações em uma amostra de que pertencem a uma categoria.
Os valores esperados representam o número de observações que seriam esperadas se as probabilidades de Poisson fossem verdadeiras. O Minitab calcula as contagens esperadas multiplicando as probabilidades de Poisson de cada categoria pelo tamanho amostral total.
Se a contagem esperada (também chamada de frequência esperada) para qualquer categoria for menor que 5, os resultados do teste podem não serem válidos. Se a contagem esperada para uma categoria são muito baixas, você deve ser capaz de combinar essa categoria com as categorias adjacentes para alcançar a contagem mínima esperada.
Por exemplo, um departamento financeiro tem cinco categorias para classificar o número de dias que as faturas estão atrasadas: 15 ou menos, 16–30, 31–45, 46–60 e 60 ou mais. A categoria para 60 dias ou mais tem uma contagem esperada baixa, por isso o departamento de finanças combina ela com a categoria para 46–60 dias para criar uma categoria combinada para 45 dias ou mais.
Interpretação
É possível comparar os valores observados e os valores esperados usando-se a tabela de saída ou o gráfico de barras. As diferenças maiores entre os valores observados e esperados indicam que os dados não seguem uma distribuição de Poisson.
Método
| Frequências em Observado |
|---|
Estatísticas Descritivas
| N | Média |
|---|---|
| 300 | 0,536667 |
Contagens observadas e esperadas para Defeitos
| Defeitos | Probabilidade de Poisson | Contagem observada | Contagem esperada | Contribuição para Qui-Quadrado |
|---|---|---|---|---|
| 0 | 0,584694 | 213 | 175,408 | 8,056 |
| 1 | 0,313786 | 41 | 94,136 | 29,993 |
| 2 | 0,084199 | 18 | 25,260 | 2,086 |
| >=3 | 0,017321 | 28 | 5,196 | 100,072 |
Teste qui-quadrado
| Hipótese nula | H₀: dados seguem uma distribuição de Poisson |
|---|---|
| Hipótese alternativa | H₁: dados não seguem uma distribuição de Poisson |
| GL | Qui-Quadrado | Valor-p |
|---|---|---|
| 2 | 140,208 | 0,000 |
Contribuição ao Qui-Quadrado
Usar a categoria de contribuições individuais para quantificar o quanto do total da estatística qui-quadrado é atribuível à divergência de cada categoria.
O Minitab calcula a contribuição de cada categoria para a estatística qui-quadrado como o quadrado da diferença entre os valores observados e esperados para uma categoria, dividido pelo valor esperado para essa categoria. A estatística qui-quadrado é a soma destes valores para todas as categorias.
Interpretação
Categorias com uma grande diferença entre os valores observados e esperados fazem uma contribuição maior para a estatística qui-quadrado global.
Método
| Frequências em Observado |
|---|
Estatísticas Descritivas
| N | Média |
|---|---|
| 300 | 0,536667 |
Contagens observadas e esperadas para Defeitos
| Defeitos | Probabilidade de Poisson | Contagem observada | Contagem esperada | Contribuição para Qui-Quadrado |
|---|---|---|---|---|
| 0 | 0,584694 | 213 | 175,408 | 8,056 |
| 1 | 0,313786 | 41 | 94,136 | 29,993 |
| 2 | 0,084199 | 18 | 25,260 | 2,086 |
| >=3 | 0,017321 | 28 | 5,196 | 100,072 |
Teste qui-quadrado
| Hipótese nula | H₀: dados seguem uma distribuição de Poisson |
|---|---|
| Hipótese alternativa | H₁: dados não seguem uma distribuição de Poisson |
| GL | Qui-Quadrado | Valor-p |
|---|---|---|
| 2 | 140,208 | 0,000 |
Nestes resultados, os valores de qui-quadrado de cada categoria somam-se à estatística qui-quadrado geral, que é 140,208. A maior contribuição vem da 3 ou mais categorias de defeitos. Este resultado indica que a maior diferença entre as contagens observadas e esperadas está em 3 ou mais categorias de defeitos. A menor diferença entre as contagens observadas e esperadas está em 2 categorias de defeitos.
Hipóteses nula e alternativa
- Hipótese nula
- A hipótese nula afirma que uma população segue uma distribuição específica. A hipótese nula é, muitas vezes, uma afirmação inicial baseada em análises anteriores ou no conhecimento especializado.
- Hipótese alternativa
- A hipótese alternativa afirma que a população não segue uma distribuição específica.
DF
Os graus de liberdade (DF) são o número de informações independentes sobre uma estatística. Os graus de liberdade para o teste da qualidade do ajuste para Poisson é o número de categorias - 2.
Interpretação
O Minitab usa os graus de liberdade para determinar a estatística de teste. Quanto mais categorias que você tem em seu estudo, mais graus de liberdade que você tem.
Qui-quadrado
A estatística qui-quadrado é um teste estatístico que mede a quantidade de divergência entre a distribuição de seus dados de amostra e uma distribuição de Poisson esperada.
Interpretação
Você pode usar a estatística de qui-quadrado para determinar se deve rejeitar a hipótese nula. No entanto, o valor-p é usado com maior frequência porque é mais fácil de ser interpretado. O valor-p é a probabilidade de se obter uma estatística de teste (como a estatística de qui-quadrado) que seja pelo menos tão extrema quanto o valor que é calculado a partir da amostra, quando os dados seguem uma distribuição de Poisson.
Para determinar se deve rejeitar a hipótese nula, compare a estatística do qui-quadrado com seus valores críticos. Se a estatística do qui-quadrado for maior que o valor crítico, você deve rejeitar a hipótese nula. Caso contrário, você não deve rejeitar a hipótese nula. É possível calcular o valor crítico no Minitab ou encontrar o valor crítico de uma tabela distribuição do qui-quadrado na maioria dos livros de estatísticas. Para obter mais informações, acesse Usando a função de distribuição cumulativa inversa (ICDF) e clique em "Usar o ICDF para calcular valores críticos".
O Minitab usa a estatística qui-quadrado para calcular o valor-p.
Valor de p
O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor de p menor fornece uma evidência mais forte contra a hipótese nula.
Interpretação
Use o valor de p para determinar se os dados não seguem uma distribuição de Poisson.
- Valor de p ≤ α: Os dados não seguem uma distribuição de Poisson (Rejeite H0)
- Se o valor de p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os seus dados não seguem a distribuição de Poisson.
- Valor de p > α: Não é possível concluir que os dados não seguem uma distribuição de Poisson (não deve rejeitar H0)
- Se o valor de p é maior do que o nível de significância, você não deve rejeitar a hipótese nula, porque não há provas suficientes para concluir que os seus dados não seguem uma distribuição de Poisson.
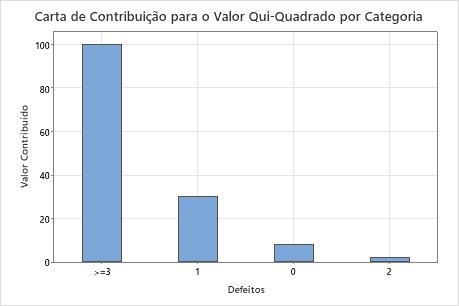
Gráfico de contribuição para o valor de qui-quadrado por categoria
Este gráfico de barras representa graficamente a contribuição de cada categoria para a estatística qui-quadrado global. Você pode escolher um gráfico que ordene as categorias por contribuição, desde a maior contribuição até a menor contribuição.
Interpretação
Categorias com uma grande diferença entre os valores observados e esperados fazem uma contribuição maior para a estatística qui-quadrado global.

Este gráfico de barras indica que a maior diferença entre os valores observados e esperados, está em 3 ou mais categorias de defeitos.
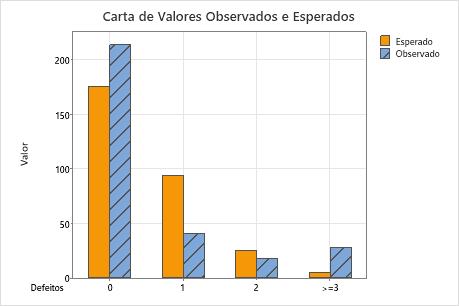
Gráfico de valores observados e esperados
Use um gráfico de barras dos valores observados e esperados para determinar se, para cada categoria, o número de valores observados é diferente do número de valores esperados. As diferenças maiores entre os valores observados e esperados indicam que os dados não seguem uma distribuição de Poisson.

Este gráfico de barras indica que os valores observados para 0 defeitos, 1 defeito, e mais de 3 defeitos são diferentes dos valores esperados. Assim, o gráfico de barras confirma visualmente o que o valor de p indica, que é que os dados não seguem uma distribuição de Poisson.
