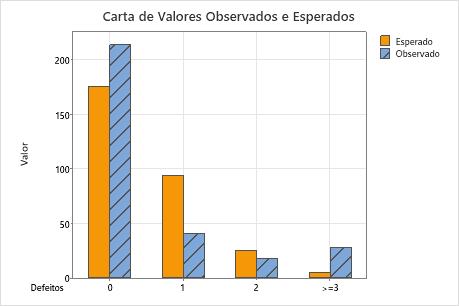
Um engenheiro de qualidade em uma empresa de produtos eletrônicos de consumo quer saber se os defeitos por aparelho de TV decorrem de uma distribuição de Poisson. O engenheiro seleciona aleatoriamente 300 TVs e registra o número de defeitos por televisão.
- Abra os dados amostrais, DefeitosDeTV.MWX.
- Selecione .
- Em Variável, insira Defeitos.
- Em Variável de frequência (opcional), insira Observado.
- Clique em OK.
Interpretar os resultados
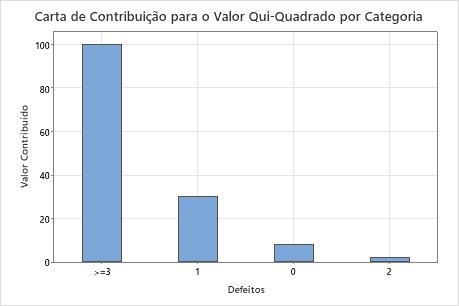
A hipótese nula afirma que os dados seguem uma distribuição de Poisson. Como o valor de p é 0,000, o que é inferior ao nível de significância de 0,05, o engenheiro rejeita a hipótese nula e conclui que os dados não seguem uma distribuição de Poisson. Os gráficos indicam que a diferença entre os valores observados e esperados é grande para as categorias 1 e  3, e que a categoria 3 é o maior contribuinte para a estatística qui-quadrado.
3, e que a categoria 3 é o maior contribuinte para a estatística qui-quadrado.
Método
| Frequências em Observado |
|---|
Estatísticas Descritivas
| N | Média |
|---|---|
| 300 | 0,536667 |
Contagens observadas e esperadas para Defeitos
| Defeitos | Probabilidade de Poisson | Contagem observada | Contagem esperada | Contribuição para Qui-Quadrado |
|---|---|---|---|---|
| 0 | 0,584694 | 213 | 175,408 | 8,056 |
| 1 | 0,313786 | 41 | 94,136 | 29,993 |
| 2 | 0,084199 | 18 | 25,260 | 2,086 |
| >=3 | 0,017321 | 28 | 5,196 | 100,072 |
Teste qui-quadrado
| Hipótese nula | H₀: dados seguem uma distribuição de Poisson |
|---|---|
| Hipótese alternativa | H₁: dados não seguem uma distribuição de Poisson |
| GL | Qui-Quadrado | Valor-p |
|---|---|---|
| 2 | 140,208 | 0,000 |