Um engenheiro de controle da qualidade precisa assegurar que as tampas em frascos de shampoo sejam fixadas corretamente. Se as tampas forem insuficientemente apertadas, elas poderão se soltar durante o transporte. Se forem excessivamente apertadas, poderão ser difíceis de remover. O valor ideal do torque para fixar as tampas é 18. O engenheiro coleta uma amostra aleatória de 68 frascos e testa o torque necessário para remover as tampas.
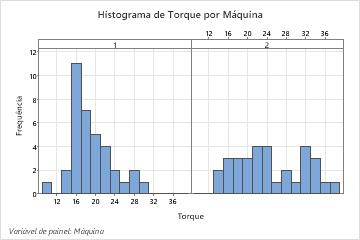
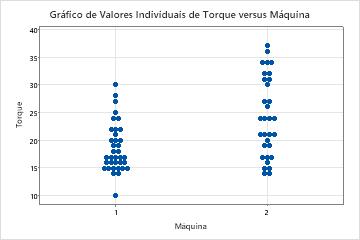
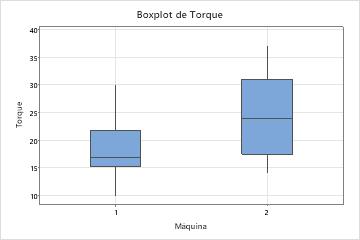
Como parte da investigação inicial, o engenheiro analisa a estatística descritiva das medições de torque para avaliar a distribuição dos dados de cada máquina.
- Abra os dados amostrais, TorqueTampa.MWX.
- Selecione .
- Em Variáveis, insira Torque.
- Em Por variáveis (opcional), insira Máquina.
- Clique no botão Gráficos e, em seguida, selecione Histograma dos dados, Gráfico de Valores Individuais e Boxplot de dados.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
O valor médio do torque para a Máquina 1 está mais próximo do alvo de 18 do que o valor de torque médio para Máquina 2. O torque médio necessário para remover as tampas da Máquina 1 é 18,667, e o torque médio necessário para remover a tampa da Máquina 2 é 24,19. A distribuição dos dados a partir da Máquina 1 também é menos variável. O desvio padrão é 4,395 para a Máquina 1 e é 7,12 para a Máquina 2.
Os gráficos mostram também que existe uma diferença nos valores de torque médio para as duas máquinas. Para determinar se existe uma diferença significativa nas médias da população, o engenheiro poderia fazer um teste t de 2 amostras.
Estatísticas
| Variável | Máquina | N | N* | Média | EP Média | DesvPad | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Torque | 1 | 36 | 0 | 18,6667 | 0,732467 | 4,39480 | 10 | 15,25 | 17 | 21,75 | 30 |
| 2 | 32 | 0 | 24,1875 | 1,25839 | 7,11852 | 14 | 17,5 | 24 | 31 | 37 |