Neste tópico
Coeficiente de correlação de Pearson
Fórmula
Mede o grau de relação linear entre duas variáveis. O coeficiente de correlação assume um valor entre -1 e +1. Se uma variável tende a aumentar à medida que as outras diminuem, o coeficiente é negativo. Por outro lado, se as duas variáveis tendem a aumentar em conjunto, o coeficiente de correlação é positivo.
Para as variáveis x e y:
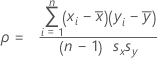
Notação
| Termo | Descrição |
|---|---|
 | média da amostra para a primeira variável |
| sx | desvio padrão da amostra para a primeira variável |
 | média da amostra para a segunda variável |
| sy | desvio padrão da amostra para a segunda variável |
| n | número de observações |
Intervalos de confiança de correlação de Pearson
O intervalo de confiança bilateral (1- α) 100% para ρ é (ρL, ρU), onde o limite inferior, pL, e o limite superior, pU, seguem:
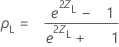
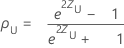
onde:


Notação
| Termo | Descrição |
|---|---|
| r | Estimativa da correlação amostral de Pearson da correlação desconhecida, ρ |
| ρ | coeficiente de correlação |
| n | número de observações |
Coeficiente de correlação de Spearman
Para o cálculo do coeficiente de correlação de Spearman e do valor de p, execute uma correlação de Pearson nos postos dos dados. Os postos de respostas empatadas são a média das postos dos empates. A tabela a seguir mostra os empates para duas amostras de dados.
| C1 | C2 | C3 | C4 |
|---|---|---|---|
| A | Posto A | B | Posto B |
| 45 | 4 | 23 | 1 |
| 78 | 6 | 25 | 3 |
| 24 | 3 | 25 | 3 |
| 51 | 5 | 25 | 3 |
| 13 | 1,5 | 34 | 6 |
| 13 | 1,5 | 30 | 5 |
O coeficiente de correlação de Spearman entre A e B é -0,678 e o valor de p é 0,139. Estes valores são idênticos aos do coeficiente e valor de p a partir de uma correlação de Pearson nos valores nos Postos A e B.
O Minitab omite linhas que contêm dados faltantes para uma ou ambas as variáveis nos cálculos. Ambas as colunas devem ter o mesmo número de linhas.
Intervalos de confiança de correlação de Spearman
O intervalo de confiança bilateral (1- α) 100% para ρ é (ρL, ρU), onde o limite inferior, pL, e o limite superior, pU, seguem:
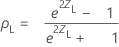
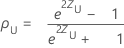
onde:


Bonnett e Wright (2000) sugerem o uso do seguinte ajuste para o erro padrão:

Notação
| Termo | Descrição |
|---|---|
| r | Estimativa da correlação amostral de Spearman da correlação desconhecida, ρ |
| ρ | coeficiente de correlação |
| n | número de linhas sem dados faltantes para o par de variáveis |
Valor-p
As hipóteses para um teste de que a correlação é 0 são as seguintes:
H0: ρ = 0 versus H1: ρ ≠ 0 onde ρ é o coeficiente de correlação de Pearson ou o coeficiente de correlação de Spearman entre um par de variáveis.
Fórmula
As estatísticas de teste para o coeficiente de correlação de Pearson e o coeficiente de correlação de Spearman têm a mesma fórmula:

O valor de p é 2 × P(T > t) onde T segue uma distribuição t com n – 2 graus de liberdade.
Notação
| Termo | Descrição |
|---|---|
| r | coeficiente de correlação da amostra |
| n | número de observações |
