Neste tópico
Etapa 1: Examine os relacionamentos entre variáveis em um gráfico de matriz
Use o gráfico de matriz para examinar os relacionamentos entre duas variáveis contínuas. Além disso, procure outliers nos relacionamentos. Os outliers podem influenciar fortemente os resultados do coeficiente de correlação de Pearson.
Determine se os relacionamentos são lineares, monótonos ou nenhum dos dois. A seguir, exemplos dos tipos de formulários que os coeficientes de correlação descrevem. O coeficiente de correlação de Pearson é apropriado para formas lineares. O coeficiente de correlação de Spearman é apropriado para formas monótonas.

Nenhuma relação
Os pontos caem aleatoriamente no gráfico, o que indica que não existe uma relação linear entre as variáveis.
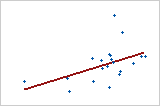
Relação positiva moderada
Alguns pontos estão perto da linha, mas outros pontos estão longe dela, o que indica apenas uma relação linear moderada entre as variáveis.
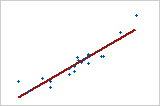
Relação positiva moderada
Os pontos caem perto da linha, o que indica que há uma forte relação linear entre as variáveis. A relação é positiva, porque conforme uma variável aumenta, a outra variável também aumenta.
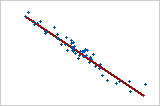
Relação negativa grande
Os pontos caem perto da linha, o que indica que há uma forte relação negativa entre as variáveis. A relação é negativa, porque, conforme uma variável aumenta, a outra variável diminui.
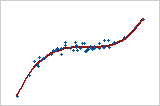
Monótono
Em uma relação monotônica, as variáveis tendem a mover-se na mesma direção relativa, mas não necessariamente a uma taxa constante. Em uma relação linear, as variáveis se movem na mesma direção, a uma taxa constante. Este Gráfico mostra as duas variáveis aumentando simultaneamente, mas não à mesma taxa. A relação é monotônica porém não linear. O coeficiente de correlação de Pearson para esses dados é 0,843, mas a correlação de Spearman é maior, 0,948.
Quadrático curvado
Este exemplo mostra um relacionamento curvo. Embora a relação entre as variáveis seja forte, o coeficiente de correlação seria próximo de zero. O relacionamento não é linear nem monótono.
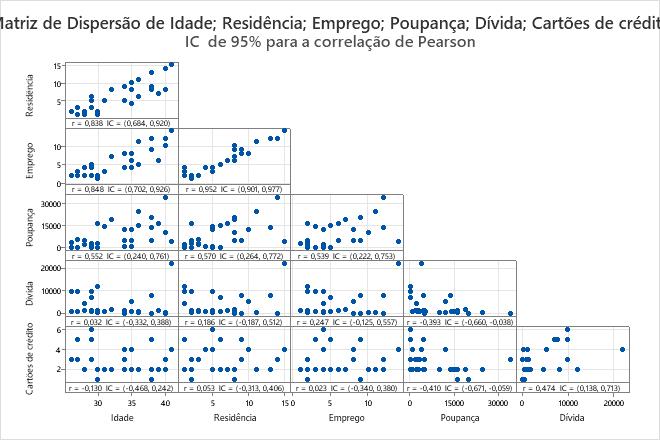
Resultado chave: Matriz de dispersão
- Existe uma forte relação linear positiva entre Empregar e Residência.
- Existe uma relação linear negativa fraca entre cartões de crédito e poupança.
- A dívida parece ter um outlier que deve ser investigado.
Etapa 2: Examine os coeficientes de correlação entre as variáveis
Use o coeficiente de correlação de Pearson para analisar a intensidade e a direção da relação linear entre duas variáveis contínuas.
- Resistência
-
O coeficiente de correlação pode variar em termos de valor de -1 a +1. Quanto maior for o valor absoluto do coeficiente, mais forte é a relação entre as variáveis.
Para a correlação de Pearson, um valor absoluto de 1 indica uma relação linear perfeita. A correlação perto de 0 indica que não há relação linear entre as variáveis. - Direção
-
O sinal de cada coeficiente indica a direção da relação. Se ambas as variáveis tendem a aumentar ou diminuir em conjunto, o coeficiente é positivo, e a linha que representa a correlação inclina para cima. Se uma variável tende a aumentar à medida que os outras diminuem, o coeficiente é negativo, e a linha que representa a correlação inclina para baixo.
- Nunca é adequado concluir que as mudanças em uma variável causam mudanças em outra variável com base apenas na correlação. Somente experimentos adequadamente controlados permitem que você determine se uma relação é causal.
- O coeficiente de correlação de Pearson é muito sensível a valores extremos de dados. Um valor único que é muito diferente dos outros valores de um conjunto de dados pode alterar significativamente o valor do coeficiente. Você deve tentar identificar a causa de qualquer valor extremo. Corrija os erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
- Um coeficiente de correlação de Pearson baixo não significa que não existe nenhuma relação entre as variáveis. As variáveis podem ter uma relação não linear.
Método
| Tipo de correlação | Pearson |
|---|---|
| Número de linhas usadas | 30 |
Correlações
| Idade | Residência | Emprego | Poupança | Dívida | |
|---|---|---|---|---|---|
| Residência | 0,838 | ||||
| Emprego | 0,848 | 0,952 | |||
| Poupança | 0,552 | 0,570 | 0,539 | ||
| Dívida | 0,032 | 0,186 | 0,247 | -0,393 | |
| Cartões de crédito | -0,130 | 0,053 | 0,023 | -0,410 | 0,474 |
Resultado principal: Correlação de Pearson
- Residência e Idade, 0,838
- Empregar e Idade, 0,848
- Empregar e Residência, 0,952
- Dívida e Poupança , -0,393
- Cartões de crédito e idade, -0,130
- Cartões de crédito e poupança, -0,410
