Neste tópico
Correlações de Pearson
A matriz de correlação mostra os valores de correlação de Pearson, que medem o grau de relação linear entre cada par de variáveis. Os valores de correlação podem cair entre -1 e +1. Se as duas variáveis tendem a aumentar e diminuir juntas, o valor de correlação é positivo. Se uma variável aumenta enquanto a outra variável diminui, o valor de correlação é negativo.
Interpretação
Use a matriz de correlação para avaliar a força e a direção da relação entre duas variáveis. Um valor de correlação alto e positivo indica que as variáveis medem a mesma característica. Se os itens não estão altamente correlacionados, os itens podem medir diferentes características ou podem não estar claramente definidos.
Correlações
| Idade | Residência | Emprego | Poupança | Dívida | |
|---|---|---|---|---|---|
| Residência | 0,838 | ||||
| Emprego | 0,848 | 0,952 | |||
| Poupança | 0,552 | 0,570 | 0,539 | ||
| Dívida | 0,032 | 0,186 | 0,247 | -0,393 | |
| Cartões de crédito | -0,130 | 0,053 | 0,023 | -0,410 | 0,474 |
- Residência e Idade, 0,838
- Empregar e Idade, 0,848
- Empregar e Residência, 0,952
- Dívida e Poupança , -0,393
- Cartões de crédito e idade, -0,130
- Cartões de crédito e poupança, -0,410
Correlações de Spearman
Use o coeficiente de correlação de Spearman para analisar a intensidade e a direção da relação monótona entre duas variáveis contínuas ou ordinais. Em uma relação monotônica, as variáveis tendem a mover-se na mesma direção relativa, mas não necessariamente a uma taxa constante. Para calcular a correlação de Spearman, o Minitab atribui postos para os dados brutos. Em seguida, o Minitab calcula o coeficiente de correlação com os dados atribuídos em postos.
- Resistência
-
O coeficiente de correlação pode variar em termos de valor de -1 a +1. Quanto maior for o valor absoluto do coeficiente, mais forte é a relação entre as variáveis.
Para a correlação de Spearman, um valor absoluto de 1 indica que os dados ordenados por posto são perfeitamente lineares. Por exemplo, uma correlação de Spearman de -1 significa que o maior valor para a variável A está associado ao menor valor para a variável B, o segundo maior valor para a variável A está associado com o segundo menor valor para a variável B, e assim por diante.
- Direção
-
O sinal de cada coeficiente indica a direção da relação. Se ambas as variáveis tendem a aumentar ou diminuir em conjunto, o coeficiente é positivo, e a linha que representa a correlação inclina para cima. Se uma variável tende a aumentar à medida que os outras diminuem, o coeficiente é negativo, e a linha que representa a correlação inclina para baixo.
Os gráficos a seguir mostram os dados com valores de coeficiente de correlação de Spearman específicos para ilustrar padrões diferentes na força e direção das relações entre as variáveis.

Nenhum relacionamento: Rô de Spearman = 0
Os pontos caem aleatoriamente no gráfico, o que indica que não existe uma relação entre as variáveis.
Forte relação positiva: Rô de Spearman = 0,948
Os pontos caem perto da linha, o que indica que há uma forte relação entre as variáveis. A relação é positiva, porque as variáveis aumentam simultaneamente.

Forte relação negativa: Rô de Spearman = -1,0
Os pontos caem perto da linha, o que indica que há uma forte relação entre as variáveis. A relação é negativa, porque, conforme uma variável aumenta, a outra variável diminui.
Nunca é adequado concluir que as mudanças em uma variável causam mudanças em outra variável com base apenas na correlação. Somente experimentos adequadamente controlados permitem que você determine se uma relação é causal.
Interpretação
Correlações
| Idade | Residência | Emprego | Poupança | Dívida | |
|---|---|---|---|---|---|
| Residência | 0,824 | ||||
| Emprego | 0,830 | 0,912 | |||
| Poupança | 0,570 | 0,571 | 0,496 | ||
| Dívida | -0,198 | -0,142 | -0,056 | -0,605 | |
| Cartões de crédito | -0,179 | 0,069 | 0,036 | -0,480 | 0,353 |
Correlações de Spearman pareadas
| Amostra 1 | Amostra 2 | N | Correlação | IC de 95% para ρ | Valor-p |
|---|---|---|---|---|---|
| Residência | Idade | 30 | 0,824 | (0,624; 0,922) | 0,000 |
| Emprego | Idade | 30 | 0,830 | (0,636; 0,926) | 0,000 |
| Poupança | Idade | 30 | 0,570 | (0,236; 0,783) | 0,001 |
| Dívida | Idade | 30 | -0,198 | (-0,524; 0,178) | 0,293 |
| Cartões de crédito | Idade | 30 | -0,179 | (-0,508; 0,197) | 0,345 |
| Emprego | Residência | 30 | 0,912 | (0,798; 0,963) | 0,000 |
| Poupança | Residência | 30 | 0,571 | (0,237; 0,784) | 0,001 |
| Dívida | Residência | 30 | -0,142 | (-0,479; 0,232) | 0,454 |
| Cartões de crédito | Residência | 30 | 0,069 | (-0,300; 0,419) | 0,719 |
| Poupança | Emprego | 30 | 0,496 | (0,144; 0,737) | 0,005 |
| Dívida | Emprego | 30 | -0,056 | (-0,408; 0,311) | 0,768 |
| Cartões de crédito | Emprego | 30 | 0,036 | (-0,328; 0,392) | 0,849 |
| Dívida | Poupança | 30 | -0,605 | (-0,804; -0,283) | 0,000 |
| Cartões de crédito | Poupança | 30 | -0,480 | (-0,726; -0,124) | 0,007 |
| Cartões de crédito | Dívida | 30 | 0,353 | (-0,020; 0,639) | 0,056 |
Nestes resultados, a correlação de Spearman entre Residência e Idade é de 0,824, o que indica que existe uma relação positiva entre as variáveis. O intervalo de confiança para rho é de 0,624 a 0,922. O valor-p é 0,000, o que indica que a relação é estatisticamente significativa ao nível α = 0,05.
A correlação de Spearman entre dívida e poupança é de -0,605 e entre cartões de crédito e poupança é de 0,480. A relação entre essas variáveis é negativa, o que indica que, como os cartões de débito e crédito aumentam, a economia diminui.
Linhas usadas
O número de linhas usadas é exibido na tabela método. É o número de linhas de dados, incluindo valores ausentes.
Quando você tem valores ausentes, o número de linhas usadas não é o mesmo que o tamanho real da amostra usado no cálculo do intervalo de confiança.
Intervalos de confiança para correlação
O intervalo de confiança fornece um intervalo de valores prováveis para os coeficientes de correlação. Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. Mas, se você repetir sua amostra várias vezes, uma determinada porcentagem dos intervalos de confiança ou limites resultantes conteria o coeficiente de correlação desconhecido. A porcentagem desses intervalos de confiança ou limites que contêm o coeficiente de correlação é o nível de confiança do intervalo.
Por exemplo, um nível de confiança de 95% indica que, se você extrair 100 amostras aleatórias da população, poderia esperar que, aproximadamente, 95 das amostras produza intervalos que contêm o coeficiente de correlação.
Uma fronteira superior define um valor provável que a diferença da população seja menor. Uma fronteira inferior define um valor provável que a diferença da população seja maior.
Os intervalos de confiança para a correlação de Pearson são sensíveis à normalidade da distribuição bivariada subjacente. Se os dados se desviarem da normalidade, os intervalos de confiança podem ser imprecisos, independentemente da magnitude do tamanho da amostra.
Os intervalos de confiança para as correlações de Spearman são baseados em classificações e são menos sensíveis à suposição de distribuição bivariada subjacente.
Interpretação
O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra. Para obter mais informações, vá para Como obter um intervalo de confiança mais preciso.
Correlações de Pearson pareadas
| Amostra 1 | Amostra 2 | N | Correlação | IC de 95% para ρ | Valor-p |
|---|---|---|---|---|---|
| Residência | Idade | 30 | 0,838 | (0,684; 0,920) | 0,000 |
| Emprego | Idade | 30 | 0,848 | (0,702; 0,926) | 0,000 |
| Poupança | Idade | 30 | 0,552 | (0,240; 0,761) | 0,002 |
| Dívida | Idade | 30 | 0,032 | (-0,332; 0,388) | 0,865 |
| Cartões de crédito | Idade | 30 | -0,130 | (-0,468; 0,242) | 0,494 |
| Emprego | Residência | 30 | 0,952 | (0,901; 0,977) | 0,000 |
| Poupança | Residência | 30 | 0,570 | (0,264; 0,772) | 0,001 |
| Dívida | Residência | 30 | 0,186 | (-0,187; 0,512) | 0,326 |
| Cartões de crédito | Residência | 30 | 0,053 | (-0,313; 0,406) | 0,779 |
| Poupança | Emprego | 30 | 0,539 | (0,222; 0,753) | 0,002 |
| Dívida | Emprego | 30 | 0,247 | (-0,125; 0,557) | 0,189 |
| Cartões de crédito | Emprego | 30 | 0,023 | (-0,340; 0,380) | 0,906 |
| Dívida | Poupança | 30 | -0,393 | (-0,660; -0,038) | 0,032 |
| Cartões de crédito | Poupança | 30 | -0,410 | (-0,671; -0,059) | 0,024 |
| Cartões de crédito | Dívida | 30 | 0,474 | (0,138; 0,713) | 0,008 |
Nestes resultados, residência e idade têm uma correlação linear positiva de 0,838. Você pode ter 95% de confiança de que o coeficiente de correlação da população está entre 0,684 e 0,920. Geralmente, quando a correlação é mais forte, o intervalo de confiança é mais estreito. Por exemplo, cartões de crédito e idade têm uma correlação fraca e o intervalo de confiança de 95% varia de -0,468 a 0,242.
Valor-p
O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor-p menor fornece uma evidência mais forte contra a hipótese nula.
Interpretação
Use o valor-p para determinar se o coeficiente de correlação é estatisticamente significativo.
- Valor-P ≤ α: A correlação é estatisticamente significativa (Rejeitar H0)
- Se o valor-p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula. Você pode concluir que a correlação é estatisticamente significativa. Use seu conhecimento especializado para determinar se a diferença é praticamente significativa. Para obter mais informações, acesse Significância estatística e prática.
- Valor-p > α: A correlação não é estatisticamente significativa (Falha ao rejeitar H0)
- Se o valor-p for maior do que o nível de significância, você não deve rejeitar a hipótese nula. Você não tem evidências suficientes para concluir que a correlação é estatisticamente significativa.
Os procedimentos do valor-p para correlação de Pearson e correlação de Spearman são robustos para desvios da normalidade. Os valores-p são geralmente precisos para n ≥ 25, independentemente da população de pais da amostra.
Correlações de Pearson pareadas
| Amostra 1 | Amostra 2 | N | Correlação | IC de 95% para ρ | Valor-p |
|---|---|---|---|---|---|
| Residência | Idade | 30 | 0,838 | (0,684; 0,920) | 0,000 |
| Emprego | Idade | 30 | 0,848 | (0,702; 0,926) | 0,000 |
| Poupança | Idade | 30 | 0,552 | (0,240; 0,761) | 0,002 |
| Dívida | Idade | 30 | 0,032 | (-0,332; 0,388) | 0,865 |
| Cartões de crédito | Idade | 30 | -0,130 | (-0,468; 0,242) | 0,494 |
| Emprego | Residência | 30 | 0,952 | (0,901; 0,977) | 0,000 |
| Poupança | Residência | 30 | 0,570 | (0,264; 0,772) | 0,001 |
| Dívida | Residência | 30 | 0,186 | (-0,187; 0,512) | 0,326 |
| Cartões de crédito | Residência | 30 | 0,053 | (-0,313; 0,406) | 0,779 |
| Poupança | Emprego | 30 | 0,539 | (0,222; 0,753) | 0,002 |
| Dívida | Emprego | 30 | 0,247 | (-0,125; 0,557) | 0,189 |
| Cartões de crédito | Emprego | 30 | 0,023 | (-0,340; 0,380) | 0,906 |
| Dívida | Poupança | 30 | -0,393 | (-0,660; -0,038) | 0,032 |
| Cartões de crédito | Poupança | 30 | -0,410 | (-0,671; -0,059) | 0,024 |
| Cartões de crédito | Dívida | 30 | 0,474 | (0,138; 0,713) | 0,008 |
Nestes resultados, existem muitos valores-p que são inferiores ao nível de significância de 0,05, o que indica que os coeficientes de correlação de Pearson são estatisticamente significativos.
Observação
Há casos em que, devido a pontos de dados extremos, o valor-p pode ser pequeno, mas o intervalo de confiança é muito grande. Por exemplo, com cartões de crédito e dívida, o IC 95% é muito amplo, mas o valor-p é pequeno. Quando você examina a matriz de dispersão, é possível ver um ponto de dados extremo.
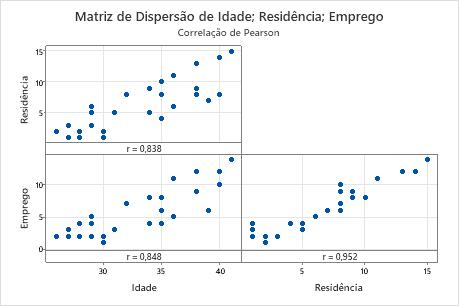
Matriz de dispersão
A matriz de dispersão é uma matriz de gráficos de dispersão. Cada gráfico de dispersão na matriz representa graficamente os escores de um par de itens nos eixos x e y.
Interpretação
Use o gráfico para avaliar visualmente a relação entre cada combinação de variáveis. As relações podem ser lineares, monótonas ou nenhuma. Use também a matriz de dispersão para procurar outliers que possam influenciar fortemente os resultados. Para mais informações sobre os tipos de relacionamentos, acesse Relações lineares, não lineares e monotônicas.
Esta matriz de dispersão sugere que todos os pares dos itens têm uma relação linear positiva.