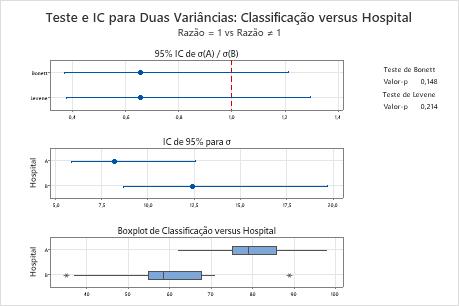
Um consultor de saúde quer comparar as classificações de satisfação do paciente de dois hospitais. O consultor coleta as classificações de 20 pacientes para cada um dos hospitais.
O consultor executa um teste de 2 variâncias para determinar se os desvios-padrão nas avaliações de pacientes de dois hospitais são diferentes.
- Abra os dados amostrais, ComparaçãoDeHospital.MWX.
- Selecione .
- Na lista suspensa, selecione As duas amostras estão em uma coluna.
- Em Amostras, insira Classificação.
- Em Identificações de Amostra, insira Hospital.
- Clique em OK.
Interpretar os resultados
A hipótese nula afirma que a relação entre os desvios-padrão é 1. Como os valores de p são ambos maiores do que o nível de significância (denotado como α ou alfa) de 0,05, o consultor não rejeita a hipótese nula. O consultor não tem evidências suficientes para concluir que os desvios padrão entre os hospitais são diferentes.
Método
| σ₁: desvio padrão de Classificação quando Hospital = A |
|---|
| σ₂: desvio padrão de Classificação quando Hospital = B |
| Razão: σ₁/σ₂ |
| Os métodos de Bonett e Levene são válidos para toda distribuição contínua. |
Estatísticas Descritivas
| Hospital | N | DesvPad | Variância | IC de 95% para σ |
|---|---|---|---|---|
| A | 20 | 8,183 | 66,958 | (5,893; 12,597) |
| B | 20 | 12,431 | 154,537 | (8,693; 19,709) |
Razão de desvios padrão
| Razão Estimada | 95% IC da Razão usando Bonett | 95% IC da Razão usando Levene |
|---|---|---|
| 0,658241 | (0,372; 1,215) | (0,378; 1,296) |
Teste
| Hipótese nula | H₀: σ₁ / σ₂ = 1 |
|---|---|
| Hipótese alternativa | H₁: σ₁ / σ₂ ≠ 1 |
| Nível de significância | α = 0,05 |
| Método | Estatística de teste | GL1 | GL2 | Valor-p |
|---|---|---|---|---|
| Bonett | 2,09 | 1 | 0,148 | |
| Levene | 1,60 | 1 | 38 | 0,214 |