Neste tópico
N
O tamanho amostral (N) é o número total de observações na amostra.
Interpretação
O tamanho amostral afeta o intervalo de confiança e o poder do teste.
Normalmente, um tamanho amostral grande resulta em um intervalo mais estreito. Uma amostra maior também proporciona ao teste mais poder para detectar uma diferença. Para obter mais informações, vá para O que é potência?.
Média
A média sumariza os valores das amostras com um único valor que representa o centro dos dados. A média é a média dos dados, que é a soma de todas as observações divididas pelo número de observações.
Interpretação
A média de cada amostra é uma estimativa da média da população de cada amostra.
StDev
O desvio padrão é a medida mais comum de dispersão, ou o quanto os dados estão dispersos sobre a média. O símbolo σ (sigma) é frequentemente usado para representar o desvio padrão de uma população, enquanto s é usado para representar o desvio padrão de uma amostra. A variação que é aleatória ou natural de um processo é frequentemente referida como ruído.
O desvio padrão usa as mesmas unidades que os dados.
Interpretação
Use o desvio padrão para determinar o grau de dispersão dos dados a partir da média. Um valor de desvio padrão mais alto indica maior dispersão nos dados. Uma boa regra de ouro de uma distribuição normal é que aproximadamente 68% dos valores estão dentro de um desvio padrão da média, 95% dos valores estão dentro de dois desvios padrão e 99,7% dos valores estão dentro de três desvios padrão.
O desvio padrão de cada amostra é uma estimativa do desvio padrão de cada população. Os desvios padrão são usados para calcular o intervalo de confiança e o valor-p. Um valor mais alto produz intervalos de confiança menos precisos (mais amplos) e testes menos poderosos.
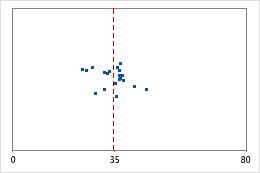
Hospital 1
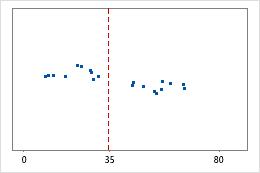
Hospital 2
Tempos de alta de hospital
Os administradores controlam o tempo gasto na alta de pacientes tratados nos departamentos de emergência de dois hospitais. Apesar de os tempos médios de alta serem quase os mesmos (35 minutos), os desvios padrão são significativamente diferentes. O desvio padrão do hospital 1 é de cerca de 6. Em média, o tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 6 minutos. O desvio padrão do hospital 2 é de cerca de 20. Na média, um tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 20 minutos.
EP Média
O erro padrão da média (SE Média) estima a variabilidade entre a amostra média que você obteria se você tivesse extraído repetidas amostras da mesma população. Considerando-se que o erro padrão da média estima a variabilidade entre as amostras, o desvio padrão mede a variabilidade dentro de uma única amostra.
Por exemplo, você tem um tempo médio de entrega de 3,80 dias, com um desvio padrão de 1,43 dias, a partir de uma amostra aleatória de 312 prazos de entrega. Estes números produzem um erro padrão da média de 0,08 dias (1,43 dividido pela raiz quadrada de 312). Se você extraiu várias amostras aleatórias do mesmo tamanho da mesma população, o desvio padrão dessas médias diferentes de amostra seria de cerca de 0,08 dias.
Interpretação
Use o erro padrão da média para determinar o quão precisamente a média da amostra estima a média da população.
Um valor menor do erro padrão da média indica uma estimativa mais precisa da média da população. Normalmente, um desvio padrão maior resulta em um erro padrão maior da média e uma estimativa menos precisa da média da população. A amostra de tamanho maior resulta em um erro padrão menor da média e uma estimativa mais precisa da média da população.
O Minitab utiliza o erro padrão da média para calcular o intervalo de confiança.
Diferença: μ1 – μ2
A diferença é a diferença desconhecida entre as médias da população que você pretende estimar. O Minitab indica qual média da população é subtraída da outra.
Estimativa para diferença
A diferença é a diferença entre as médias das duas amostras.
Como a diferença média está baseada em dados das amostras e não na população total, é improvável que a diferença da amostra seja igual à diferença da população. Para estimar melhor a diferença da população, use o intervalo de confiança da diferença.
Intervalo de confiança (IC) e limites
O intervalo de confiança fornece um intervalo de valores possíveis para a diferença da população. Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. Porém, se você repetir sua amostra muitas vezes, uma certa porcentagem dos intervalos ou fronteiras de confiança resultantes contém a diferença de população desconhecida. A porcentagem destes intervalos de confiança ou fronteiras que contêm a diferença é o nível de confiança do intervalo. Por exemplo, um nível de confiança de 95% indica que, se você extrair 100 amostras aleatórias da população, poderia esperar que, aproximadamente, 95 das amostras produza intervalos que contêm a diferença da população.
Uma fronteira superior define um valor provável que a diferença da população seja menor. Uma fronteira inferior define um valor provável que a diferença da população seja maior.
O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra. Para obter mais informações, vá para Como obter um intervalo de confiança mais preciso.
Estimativa da diferença
| Diferença | IC de 95% para a Diferença |
|---|---|
| 21,00 | (14,22; 27,78) |
Nesses resultados, a estimativa da diferença da população em médias, em taxas hospitalares é de 21. Você pode ter 95% de confiança de que a média da população para a diferença está entre 14,22 e 27,78.
Hipótese nula e hipótese alternativa
- Hipótese nula
- A hipótese nula afirma que um parâmetro da população (como a média, o desvio padrão, e assim por diante) é igual a um valor hipotético. A hipótese nula é, muitas vezes, uma afirmação inicial baseado em análises anteriores ou no conhecimento especializado.
- Hipótese alternativa
- A hipótese alternativa afirma que um parâmetro da população é menor, maior ou diferente do valor hipotético na hipótese nula. A hipótese alternativa é aquela que você acredita que pode ser verdadeira ou espera provar ser verdadeira.
Na saída, as hipóteses nula e alternativa ajudam a verificar se você inseriu o valor correto para a diferença do teste.
Valor-t
O valor-t é o valor observado da estatística do teste t que mede a diferença entre uma estatística da amostra observada e seu parâmetro de população hipotético em unidades de erro padrão.
Interpretação
Você pode comparar o valor-t a valores críticos da distribuição-t a fim de determinar se deve rejeitar a hipótese nula. No entanto, o uso do valor-p do teste para fazer a mesma determinação é geralmente mais prático e conveniente.
Para determinar se a hipótese nula deve ser rejeitada, compare o valor-t com o valor crítico. Quando assumem-se variâncias iguais, o valor crítico é tα/2, n+m–2 para um teste bilateral e tα, n+m–2 para um teste unilateral. Quando não é possível assumir variâncias iguais, o valor crítico é tα/2, r para um teste bilateral e tα, r para um teste unilateral em que r representa os graus de liberdade. Para um teste bilateral, se o valor absoluto do valor t é maior do que o valor crítico, você deve rejeitar a hipótese nula. Caso contrário, você não deve rejeitar a hipótese nula. É possível calcular o valor crítico no Minitab ou encontrar o valor crítico de uma tabela distribuição-t na maioria dos livros de estatísticas. Para obter mais informações, acesse Usando a função de distribuição cumulativa inversa (ICDF) e clique em "Usar o ICDF para calcular valores críticos".
Valor p
O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Um valor de p menor fornece uma evidência mais forte contra a hipótese nula.
Interpretação
Use o valor de p para determinar se a diferença de médias da população é estatisticamente significativa.
- Valor de p ≤ α: A diferença entre as médias é estatisticamente significativa (rejeite H0)
- Se o valor de p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula. É possível concluir que a diferença entre as médias da população não é igual à diferença hipotética. Se você não especificar uma diferença hipotética, o Minitab testa se não há diferença entre as médias (Diferença hipotética = 0)
- Valor de p > α: A diferença entre as médias não é estatisticamente significativa (não deve rejeitar H0)
- Se o valor de p for maior do que o nível de significância, você não deve rejeitar a hipótese nula. Não há evidências suficientes para concluir que a diferença entre as médias da população é estatisticamente significativa. Certifique-se de que o teste tenha poder suficiente para detectar uma diferença que seja significativa na prática. Para obter mais informações, acesse Poder e tamanho de amostra para teste t para 2 amostra.
DF
Os graus de liberdade (DF) indicam a quantidade de informações que estão disponíveis em seus dados para estimar os valores de parâmetros desconhecidos e calcular a variabilidade dessas estimativas. Para um teste t de 2 amostras, os graus de liberdade são determinados pelo número de observações em sua amostra e também depende se você pode ou não assumir variâncias iguais.
Interpretação
O Minitab usa os graus de liberdade para determinar a estatística de teste. Os graus de liberdade são determinados pelo tamanho amostral. Aumentar o tamanho da amostra fornece mais informações sobre a população, que aumenta os graus de liberdade.
StDev combinado
O desvio padrão combinado é uma estimativa do desvio padrão comum para ambas as amostras. Desvio padrão combinado é o desvio padrão de todos os pontos de dados em torno de sua média de grupo (não em torno da média global). Os grupos maiores têm uma influência proporcionalmente maior sobre a estimativa global do desvio padrão combinado.
Interpretação
O desvio padrão combinado é usado para calcular o intervalo de confiança e o valor de p.
Um valor de desvio padrão mais alto indica maior dispersão nos dados. Um valor mais alto produz intervalos de confiança menos precisos (mais amplos) e testes menos poderosos.
Exemplo de desvio padrão combinado
| Grupo | Média | Desvio Padrão | N |
|---|---|---|---|
| 1 | 9,7 | 2,5 | 50 |
| 2 | 17,3 | 6,8 | 200 |
O primeiro grupo (n = 50) tem um desvio padrão de 2,5. O segundo grupo é muito maior (n = 200) e tem um desvio padrão mais elevado (6,8). Como o desvio padrão combinado utiliza uma média ponderada, o seu valor está mais próximo do desvio padrão do maior grupo. Se você usou uma média simples, ambos os grupos tiveram efeito igual.
Gráfico de valores individuais
Um gráfico de valores individuais exibe os valores individuais em cada amostra. Um gráfico de valores individuais facilita a comparação das amostras. Cada círculo representa uma observação. Um gráfico de valores individuais é especialmente útil quando você tem relativamente poucas observações e também precisa avaliar o efeito de cada observação.
Interpretação
Utilize um gráfico de valores individuais para examinar a dispersão dos dados e identificar os outliers potenciais. Os gráficos de valores individuais são melhores quando o tamanho amostral for inferior a 50.
- Dados Assimétricos
-
Examine a dispersão de seus dados para determinar se eles parecem ser assimétricos. Quando os dados são assimétricos, a maioria dos dados está localizada no lado alto ou baixo do gráfico. Muitas vezes, é mais fácil detectar a assimetria com um histograma ou boxplot.
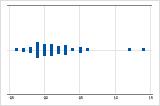
Assimétrico à direita
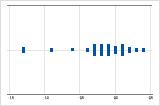
Assimétrico à esquerda
O gráfico de valores individuais com dados assimétricos à direita mostra os tempos de espera. A maioria dos tempos de espera são relativamente curtos e apenas alguns tempos de espera são longos. O gráfico de valores individuais com dados assimétricos à esquerda mostram dados de tempo de falha. Alguns itens falham imediatamente e muitos outros itens falham posteriormente.
Os dados que são extremamente assimétricos podem afetar a validade do valor de p se a suas amostras forem pequenas (ou se a amostra for inferior a 15 valores). Se seus dados forem extremamente assimétricos e você tiver uma amostra pequena, considere aumentar o tamanho amostral.
- Outliers
-
Outliers, que são valores de dados que estão distantes de outros valores de dados, podem afetar fortemente os resultados de sua análise. Muitas vezes, os outliers são mais fáceis de serem identificados em um boxplot.
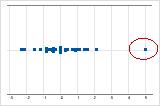
Em um gráfico de valores individuais, os valores de dados anormalmente baixos ou altos indicam possíveis outliers.
Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais). Depois, repita a análise. Para obter mais informações, acesse Identificação de outliers.
Boxplot
Um boxplot fornece um resumo gráfico da distribuição de cada amostra. O boxplot facilita a comparação da forma, da tendência central e da variabilidade das amostras.
Interpretação
Utilize um boxplot para examinar a dispersão dos dados e identificar todos os outliers potenciais. Os boxplots são melhores quando o tamanho amostral for superior a 20.
- Dados Assimétricos
-
Examine a dispersão de seus dados para determinar se eles parecem ser assimétricos. Quando os dados são assimétricos, a maioria dos dados está localizada no lado alto ou baixo do gráfico. Muitas vezes, é mais fácil detectar a assimetria com um histograma ou boxplot.
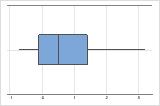
Assimétrico à direita
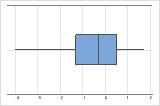
Assimétrico à esquerda
O boxplot com dados assimétricos à direita mostra os tempos de espera. A maioria dos tempos de espera são relativamente curtos e apenas alguns tempos de espera são longos. O boxplot com dados assimétricos à esquerda mostram dados de tempo de falha. Alguns itens falham imediatamente e muitos outros itens falham posteriormente.
Os dados que são extremamente assimétricos podem afetar a validade do valor de p se a suas amostras forem pequenas (ou se a amostra for inferior a 15 valores). Se seus dados forem extremamente assimétricos e você tiver uma amostra pequena, considere aumentar o tamanho amostral.
- Outliers
-
Outliers, que são valores de dados que estão distantes de outros valores de dados, podem afetar fortemente os resultados de sua análise. Muitas vezes, os outliers são mais fáceis de serem identificados em um boxplot.
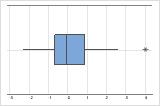
Em um boxplot, asteriscos (*) denotam outliers.
Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados para eventos anormais de ocorrência única (também chamados de causas especiais). Depois, repita a análise. Para obter mais informações, acesse Identificação de outliers.
