Métodos e fórmulas para Teste da taxa de Poisson para 2 amostras

Selecione o método ou a fórmula de sua escolha.

Neste tópico

Estatísticas
Teste de hipótese para a diferença nas taxas para a aproximação normal
Teste de hipótese para a diferença nas taxas para o método exato
Teste de hipótese para a diferença nas taxas com o método de taxa combinada
Teste de hipótese para uma diferença na média para o método de aproximação normal
Teste de hipótese para a diferença nas diferenças para o método exato
Teste de hipótese para a diferença nas médias para o método da média combinada
Intervalo de confiança para a diferença nas taxas
Limites de confiança para a diferença nas taxas
Intervalo de confiança para a diferença nas médias
Limites de confiança para a diferença nas médias

Estatísticas

O Minitab gera as estatísticas descritivas a seguir relacionadas à sua amostra. O Minitab exibe uma média somente se você alterar o "comprimento" de seu valor padrão de 1.

Termo	Descrição
taxa de ocorrência para a amostra i

Termo	Descrição
número médio de ocorrências na amostra i

Teste de hipótese para a diferença nas taxas para a aproximação normal

Fórmula

O teste de aproximação normal baseia-se na seguinte estatística de Z, que é aproximadamente distribuída como uma distribuição normal padrão sob a hipótese nula.

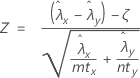
O Minitab usa as equações de valor de p para as respectivas hipóteses alternativas:

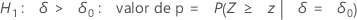
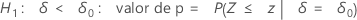
Notação

Termo	Descrição
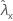	valor observado da taxa para a amostra de X
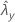	valor observado da taxa para a amostra de Y
ζ	valor verdadeiro da diferença entre as taxas de população de duas amostras
ζ₀	valor hipotético da diferença entre as taxas da população de duas amostras
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y
t_x	comprimento da amostra X
t_y	comprimento da amostra Y

Teste de hipótese para a diferença nas taxas para o método exato

Fórmula

Quando a diferença hipotética é igual a 0, o Minitab usa um procedimento exato para testar a hipótese nula a seguir:

H₀: ζ = λ_x – λ_y = 0 ou H₀: λ_x = λ_y

O procedimento exato baseia-se no fato a seguir, assumindo-se que a hipótese nula é verdadeira:

S | W ~ Binomial(w, p)

em que:

W = S + U

O Minitab usa as equações de valor de p para as respectivas hipóteses alternativas:

H₁: ζ > 0: valor de p = P(S ≥ s | w = s + u, p = p₀)
H₁: ζ < 0: valor de p = P(S ≤ s | w = s + u, p = p₀)
H₁: ζ ≠ 0:
- se P(S ≤ s | w = s + u, p = p₀) ≤ 0,5 ou P(S ≥ s | w = s + u, p = p₀) ≤ 0,5
  então, o valor de p = 2 × min {P(S ≤ s | w = s + u, p = p₀), P(S ≥ s | w = s + u, p = p₀)}
- senão, o valor de p = 1,0

em que:

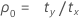
Notação

Termo	Descrição
	valor observado da taxa para a amostra de X
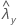	valor observado da taxa para a amostra de Y
λ_x	valor verdadeiro da taxa para a população X
λ_y	valor verdadeiro da taxa para a população Y
ζ	valor verdadeiro da diferença entre as taxas de população de duas amostras
t_x	comprimento da amostra X
t_y	comprimento da amostra Y
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y

Teste de hipótese para a diferença nas taxas com o método de taxa combinada

Quando você testar uma diferença de zero com a seguinte hipótese nula, você tem a opção de usar uma taxa combinada para ambas as amostras:

Fórmula

O procedimento de taxa combinada se baseia na seguinte estatística de Z, que é aproximadamente distribuída como uma distribuição normal padrão sob a seguinte hipótese nula:

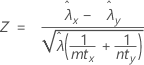
em que:

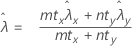
O Minitab usa as equações de valor de p para as respectivas hipóteses alternativas:

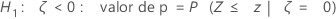
Notação

Termo	Descrição
	valor observado da taxa para a amostra de X
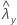	valor observado da taxa para a amostra de Y
λ_x	valor verdadeiro da taxa para a população X
λ_y	valor verdadeiro da taxa para a população Y
ζ	valor verdadeiro da diferença entre as taxas de população de duas amostras
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y
t_x	comprimento da amostra X
t_y	comprimento da amostra Y

Teste de hipótese para uma diferença na média para o método de aproximação normal

Fórmula

O teste de aproximação normal baseia-se na seguinte estatística de Z, que é aproximadamente distribuída como uma distribuição normal padrão sob a hipótese nula.

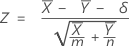
O Minitab usa as equações de valor de p para as respectivas hipóteses alternativas:

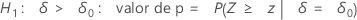
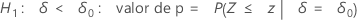
Notação

Termo	Descrição
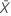	valor observado do número médio de ocorrências na amostra X
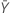	valor observado do número médio de ocorrências na amostra Y
δ	valor verdadeiro da diferença entre as médias da população de duas amostras
δ ₀	valor hipotético da diferença entre as médias da população de duas amostras
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y

Teste de hipótese para a diferença nas diferenças para o método exato

Fórmula

Quando a diferença hipotética é igual a 0, o Minitab usa um procedimento exato. O procedimento exato usa a hipótese nula a seguir:

O procedimento exato baseia-se no fato a seguir, assumindo-se que a hipótese nula é verdadeira:

S | W ~ Binomial(w, p)

em que:

W = S + U

O Minitab usa as equações de valor de p para as respectivas hipóteses alternativas:

H₁: δ > 0: valor de p = P(S ≥ s | w = s + u, δ = 0)

H₁: δ < 0: valor de p = P(S ≤ s | w = s + u, δ = 0)

H₁: δ ≠ 0:

se P(S ≤ s|w = s + u, δ = 0) ≤ 0,5

ou P(S ≥ s|w = s + u, δ = 0) ≤ 0,5

então:
senão, o valor de p = 1,0

Um teste bilateral não é um teste de igualdade de cauda, a menos que m = n.

Notação

Termo	Descrição
μ_x	o verdadeiro valor do número médio de ocorrências na população X
μ_y	o verdadeiro valor do número médio de ocorrências na população Y
δ	valor verdadeiro da diferença entre as populações médias de duas amostras
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y

Teste de hipótese para a diferença nas médias para o método da média combinada

Fórmula

Quando você testar uma diferença de zero com a seguinte hipótese nula, você tem a opção de usar uma taxa combinada para ambas as amostras:

O procedimento de média combinada se baseia no seguinte valor de Z, que é aproximadamente distribuída como uma distribuição normal padrão sob a seguinte hipótese nula:

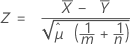
em que:

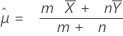
O Minitab usa as equações de valor de p para as respectivas hipóteses alternativas:

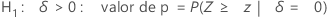
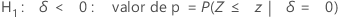
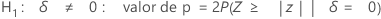
Notação

Termo	Descrição
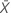	valor observado do número médio de ocorrências na amostra X
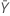	valor observado do número médio de ocorrências na amostra Y
µ_x	o verdadeiro valor do número médio de ocorrências na população X
µ_y	o verdadeiro valor do número médio de ocorrências na população Y
δ	valor verdadeiro da diferença entre as populações médias de duas amostras
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y

Intervalo de confiança para a diferença nas taxas

Fórmula

Um intervalo de confiança de 100(1 – α)% para a diferença entre as taxas de duas populações de Poisson é dada por:

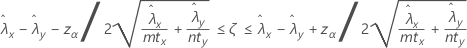
Notação

Termo	Descrição
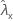	valor observado da taxa para a amostra de X
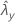	valor observado da taxa para a amostra de Y
ζ	valor verdadeiro da diferença entre as taxas de população de duas amostras
z_x	o ponto percentil superior x da distribuição normal padrão, em que 0 < x < 1
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y
t_x	comprimento da amostra X
t_y	comprimento da amostra Y

Limites de confiança para a diferença nas taxas

Fórmula

Quando você especifica um teste "maior que", um limite de confiança inferior de 100(1 – α)% para a diferença entre as taxas de duas populações de Poisson é dada por:

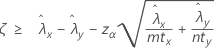
Quando você especifica um teste "menor que", um limite de confiança superior de 100(1 – α)% para a diferença entre as taxas de duas populações de Poisson é dada por:

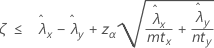
Notação

Termo	Descrição
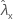	valor observado da taxa para a amostra de X
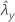	valor observado da taxa para a amostra de Y
ζ	valor verdadeiro da diferença entre as taxas de população de duas amostras
z_x	o ponto percentil superior x da distribuição normal padrão, em que 0 < x < 1
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y
t_x	comprimento da amostra X
t_y	comprimento da amostra Y

Intervalo de confiança para a diferença nas médias

Fórmula

Um intervalo de confiança de 100(1 – α)% para a diferença entre as taxas de duas populações médias de Poisson é dada por:

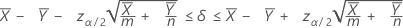
Notação

Termo	Descrição
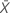	valor observado do número médio de ocorrências na amostra X
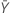	valor observado do número médio de ocorrências na amostra Y
δ	valor verdadeiro da diferença entre as populações médias de duas amostras
z_x	o ponto percentil superior x da distribuição normal padrão, em que 0 < x < 1
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y

Limites de confiança para a diferença nas médias

Fórmula

Quando você especifica um teste "maior que", um limite de confiança inferior de 100(1 – α)% para a diferença entre as médias de duas populações de Poisson é dada por:

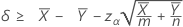
Quando você especifica um teste "menor que", um limite de confiança superior de 100(1 – α)% para a diferença entre as médias de duas populações de Poisson é dada por:

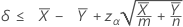
Notação

Termo	Descrição
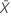	valor observado do número médio de ocorrências na amostra X
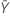	valor observado do número médio de ocorrências na amostra Y
δ	valor verdadeiro da diferença entre as populações médias de duas amostras
z_x	o ponto percentil superior x da distribuição normal padrão, em que 0 < x < 1
m	tamanho amostral da amostra X
n	tamanho amostral da amostra Y