Selecione o método ou a fórmula de sua escolha.
Intervalo de confiança (IC)
Fórmula
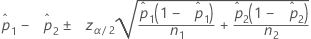
Notação
| Termo | Descrição |
|---|---|
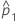 | estimativa da primeira proporção da população |
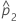 | estimativa da segunda proporção da população |
| n1 | número de ensaios na primeira amostra |
| n2 | número de ensaios na segunda amostra |
| zα/2 | probabilidade acumulada inversa da distribuição normal padrão em 1 – α/2. |
| α | 1 – nível de confiança/100 |
Teste de aproximação normal
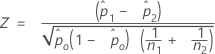
O cálculo da estatística de teste, Z, depende do método utilizado para estimar p.
- Estimativas separadas de p
- Por padrão, o Minitab utiliza estimativas separadas de p para cada população e calcula Z da seguinte maneira:
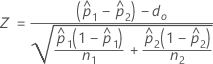
- Estimativa combinada de p
- Se a diferença de teste hipotética é zero e você opta por usar uma estimativa combinada de p para o teste, o Minitab calcula Z da seguinte maneira:
O valor de p para cada hipótese alternativa é:
- H1: p1 > p2 : valor de p = P(Z1 ≥ z)
- H1: p1 < p2 : valor de p = P(Z1 ≤ z)
- H1: p1 ≠ p2 : valor de p = 2P(Z1 ≥ z)
Calcula essas probabilidades sobre a distribuição normal padrão.
Notação
| Termo | Descrição |
|---|---|
| p1 | proporção verdadeira de eventos na primeira população |
| p2 | proporção verdadeira de eventos na segunda população |
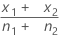
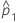 | proporção observada de eventos na primeira amostra |
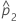 | proporção observada de eventos na segunda amostra |
| n1 | número de ensaios na primeira amostra |
| n2 | número de ensaios na segunda amostra |
| d0 | diferença hipotética entre a primeira e a segunda proporções |
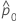 |  |
| x1 | número de eventos no primeiro exemplo |
| x2 | número de eventos no segundo exemplo |
Teste exato de Fisher
Minitab executa o teste exato de Fisher além de um teste com base em uma aproximação normal. O teste exato de Fisher é válida para todos os tamanhos amostrais.
Fórmula
Sob a hipótese nula, o número de eventos na primeira amostra (x1) tem uma distribuição hipergeométrica com estes parâmetros:
- Tamanho da população = n1 + n2
- Número de eventos na população = x1 + x2
- Tamanho amostral = n1
Permita que f( ) e F( ) denotem o PDF e FDA desta distribuição hipergeométrica, respectivamente. Permita que Mode denote seu modo. Os valores de p para cada hipótese alternativa são os seguintes:
- H1: p1 < p2
valor de p = F(x1)
- H1: p1 > p2
valor de p = 1 – F(x1 – 1)
- H1: p1 ≠ p2
Há três casos:
- Caso 1: x1 < Mode
valor de p = p inferior + p superior
Termo Descrição p inferior F(x1) p superior 1 – F(y – 1) y menor inteiro > Modo tal que f(y) <f(x1) Observação
p superior pode ser igual a zero.
- Caso 2: x1 = Modo
valor de p = 1,0
- Caso 3: x1 > Modo
valor de p = p inferior + p superior
Termo Descrição p superior 1 – F(x1 – 1) p inferior F(y) y maior inteiro < Modo tal que f(y) < f(x1) Observação
p inferior pode ser igual a zero.
- Caso 1: x1 < Mode
Notação
| Termo | Descrição |
|---|---|
| p1 | proporção verdadeira de eventos na primeira população |
| p2 | proporção verdadeira de eventos na segunda população |
| x1 | número de eventos no primeiro exemplo |
| x2 | número de eventos no segundo exemplo |
| n1 | número de ensaios na primeira amostra |
| n2 | número de ensaios na segunda amostra |
