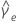Neste tópico
Desvio padrão (StDev)
O desvio padrão é a medida mais comum de dispersão, ou o quanto os dados estão dispersos sobre a média. O desvio padrão da amostra é igual à raiz quadrada da variância da amostra.
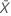 , então, o desvio padrão é dado por:
, então, o desvio padrão é dado por:

Notação
| Termo | Descrição |
|---|---|
| xi | a ia observação em sua amostra |
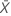 | a média da amostra |
| S | o desvio padrão da amostra |
| n | tamanho médio |
Variância
A variância mede o quanto os dados estão dispersos em relação à sua média. A variância é igual ao desvio padrão ao quadrado.
Fórmula
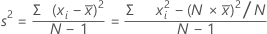
Notação
| Termo | Descrição |
|---|---|
| xi | ia observação |
 | média das observações |
| N | número de observações não ausentes |
Intervalos de confiança e limites para o método qui-quadrado
Intervalos de confiança
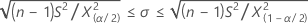

Limites de confiança
Quando você especifica um teste unilateral, o Minitab calcula um limite de confiança unilateral de 100 (1-α)%, de acordo com a direção da hipótese alternativa.
- Se você especificar uma hipótese alternativa "maior que", um limite inferior 100(1-α)% para o desvio padrão da população é dado por:

Um limite inferior de 100(1–α)% para a variância da população é dado por:
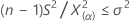
- Se você especificar uma hipótese alternativa "menor que", um limite superior de 100(1 - α)% para o desvio padrão da população é dado por:

Um limite superior de 100(1–α)% para a variância da população é dado por:

Notação
| Termo | Descrição |
|---|---|
| α | o nível alfa para o intervalo de confiança 100(1 – α)% |
| n | tamanho médio |
| S2 | variância da amostra |
| Χ2(p) | o 100po ponto de percentil em uma distribuição qui-quadrado com (n – 1) graus de liberdade |
| σ | valor verdadeiro do desvio padrão da população |
| σ2 | valor verdadeiro da variância da população |
Intervalos de confiança e limites para o método Bonett
Utilize este método para todos os dados contínuos (normal ou anormal). 1
Intervalo de confiança

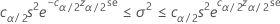
Limites de confiança
Quando você especifica um teste unilateral, o Minitab calcula um limite de confiança unilateral de 100 (1-α)%, de acordo com a direção da hipótese alternativa.
-
Se você especificar uma hipótese alternativa "maior que", um limite inferior 100(1-α)% para o desvio padrão da população é dado por:
 Um limite inferior aproximado de 100 (1- a)% para a variância da população é dado por:
Um limite inferior aproximado de 100 (1- a)% para a variância da população é dado por:
-
Se você especificar uma hipótese alternativa "menor que", um limite superior aproximado de 100(1 - α)% para o desvio padrão da população é dado por:
 Um limite superior aproximado de 100(1- a)% para a variância da população é dado por:
Um limite superior aproximado de 100(1- a)% para a variância da população é dado por: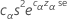
Notação
| Termo | Descrição |
|---|---|
| α | 1 – nível de confiança / 100 |
| cα/2 | n / (n – zα/2) |
| cα | n / (n – zα ) |
| s2 | valor observado da variância da amostra |
| zα/2 | probabilidade acumulada inversa da distribuição normal padrão em 1 – α/2. Se n for menor ou igual a zα/2, o Minitab não calcula os intervalos de confiança de Bonett. |
| zα | probabilidade acumulada inversa da distribuição normal padrão em 1 – α. Se n for menor ou igual a zα , o Minitab não calcula os intervalos de confiança de Bonett. |
| se |  |
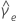 | 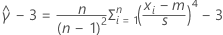 = excesso de curtose estimado = excesso de curtose estimado |
| m | média aparada com proporção de corte igual a  ; m = média da amostra quando n é menor ou igual a 5 ; m = média da amostra quando n é menor ou igual a 5 |
| σ | valor verdadeiro do desvio padrão da população |
| σ2 | valor verdadeiro da variância da população |
Teste de hipótese para o método qui-quadrado
Fórmula
O teste de hipótese usa as equações do valor de p a seguir para as respectivas hipóteses alternativas:
H1: σ2 > σ02: valor de p = P(Χ2 ≥ x2)
H1: σ2 < σ02: valor de p = P(Χ2 ≤ x2)
H1: σ2 ≠ σ02: valor de p = 2 × min{P(Χ2 ≤ x2), P(Χ2 ≥ x2)}
Notação
| Termo | Descrição | ||||||
|---|---|---|---|---|---|---|---|
| σ2 | valor verdadeiro da variância da população | ||||||
| σ02 | valor hipotético da variância da população | ||||||
| Χ2 | segue uma distribuição qui-quadrado com (n – 1) graus de liberdade quando σ2 = σ02 | ||||||
| x2 | 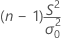
|
Teste de hipótese para o método de Bonett
Fórmula
O procedimento de Bonett não está associado a um teste estatístico. No entanto, o Minitab utiliza as regiões de rejeição definidas pelos limites de confiança para calcular um valor de p.
Para a hipótese bilateral, o valor de p é dado por:
p = 2 × min(αL, αU)
- Para uma hipótese alternativa unilateral com "menor que", o valor de p é calculado como αU depois de substituir α/2 por α na notação.
- Para uma hipótese alternativa unilateral com "maior que", o valor de p é calculado como αL depois de substituir α/2 por α na notação.
Notação
| Termo | Descrição | ||||||
|---|---|---|---|---|---|---|---|
| σ02 | variância hipotética | ||||||
| αL | menor solução, α, da equação
 | ||||||
| αU | menor solução, α, da equação
 | ||||||
| cα/2 | n / (n – zα/2) | ||||||
| α | 1 – nível de confiança / 100 | ||||||
| s2 | valor observado da variância da amostra | ||||||
| zα/2 | probabilidade acumulada inversa da distribuição normal padrão em 1 – α/2. Se n for menor ou igual a zα/2, o Minitab não calcula os intervalos de confiança de Bonett. | ||||||
| se | 
|