Neste tópico
Estatísticas
| Termo | Descrição |
|---|---|
| taxa de ocorrência |
 |
| ocorrência média |
 |
A taxa é igual ao número médio de ocorrências por comprimento unitário de observação. A média é o número médio de ocorrências em toda a amostra. Se o comprimento é igual a 1, então a taxa e a média e são iguais.
Valor de P para teste exato
Fórmula
- H1: λ > λ0: valor de p = P(S ≥ s | λ = λ0) em que S tem uma distribuição de Poisson com média nλ0t.
- H1: λ < λ0: valor de p = P(S ≤ s | λ = λ0) em que S tem uma distribuição de Poisson com média nλ0t.
- H1: λ ≠ λ0: o Minitab usa um teste da razão de verossimilhança como a seguir:
Define a função G(s), que expressa o teste da razão de verossimilhança em termos de s, o número total de ocorrências no processo de Poisson:

- se 0 ≤ s < nλ0t, resolve a equação G(y) = G(s) para y no intervalo (nλ0t, enλ0t];
o valor de p = P(S ≤ s | λ = λ0) + P(S ≥ y | λ = λ0)
- se s = nλ0t, então
valor de p = 1,00
- se nλ0t < s ≤ enλ0t, resolve a equação G(y) = G(s) para y no intervalo [0, nλ0t);
valor de p = P(S ≤ y | λ = λ0) + P(S ≥ s | λ = λ0)
- se s > enλ0t, o teste é unilateral e
valor de p = P(S ≥ s | λ = λ0)
onde S tem uma distribuição de Poisson com média nλ0t.
- se 0 ≤ s < nλ0t, resolve a equação G(y) = G(s) para y no intervalo (nλ0t, enλ0t];
Notação
| Termo | Descrição |
|---|---|
| s | o número médio de ocorrências total no processo de Poisson |
| t | "comprimento" da observação |
| λ0 | valor hipotético do parâmetro da taxa da população |
| λ | valor verdadeiro do parâmetro da taxa para a população |
| n | tamanho médio |
| e | 2,71828, aproximadamente |
Intervalos de confiança e limites de confiança para o teste exato
Intervalos de confiança
Um intervalo de confiança exato 100(1 – α)% para a taxa de ocorrência de um processo de Poisson é dada por:
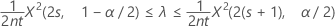
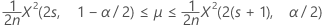
Limites de confiança
Quando você especifica um teste unilateral, o Minitab calcula um limite de confiança unilateral de 100 (1 - α)%, de acordo com a direção da hipótese alternativa.
-
Se você especificar uma hipótese alternativa "maior que", um limite inferior exato 100(1 - α)% da taxa é dado por:
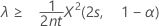
O limite inferior exato de de 100(1 – α)% da média é dado por:
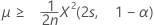
-
Se você especificar uma hipótese alternativa "menor que", um limite superior exato 100(1 - α)% da taxa é dado por:
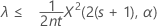
O limite superior exato de de 100(1 – α)% da média é dado por:
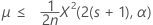
Notação
| Termo | Descrição |
|---|---|
| s | o número médio de ocorrências total no processo de Poisson |
| t | "comprimento" da observação |
| λ | valor verdadeiro da taxa para a população |
| μ | valor verdadeiro da média da população |
| Χ2(p) | ponto percentil superior x da distribuição Χ2 com p graus de liberdade, onde 0 < x < 1. |
| α | o nível alfa para o intervalo de confiança 100(1 – α)% |
| n | tamanho médio |
Valor de p para aproximação normal
Aproximações normais são válidas se o número total de ocorrências for maior do que 10.
Fórmula
O teste baseado na hipótese de uma aproximação normal para Teste da taxa de Poisson para 1 amostra utiliza as seguintes equações de valor de p para as respectivas hipóteses alternativas:


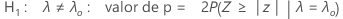
Notação
| Termo | Descrição |
|---|---|
| Z | 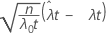 |
| t | "comprimento" da observação |
| λ 0 | valor hipotético do parâmetro da taxa da população |
| λ | valor verdadeiro do parâmetro da taxa para a população |
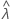 | valor observado da estatística da taxa para a amostra |
| n | tamanho médio |
Intervalos de confiança e limites de confiança para aproximação normal
Intervalos de confiança
Um intervalo de confiança de 100(1 – α)%, com base em uma aproximação normal, para a taxa de ocorrência de um processo de Poisson é dada por:
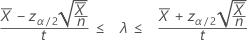
Quando você especifica um valor de "comprimento", o Minitab também exibe um intervalo de confiança para a média do número de ocorrências. Esse intervalo de confiança é dado por:
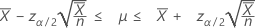
Limites de confiança
Quando você especifica um teste unilateral, o Minitab calcula um limite de confiança unilateral de 100 (1 - α)%, de acordo com a direção da hipótese alternativa.-
Se você especificar uma hipótese alternativa "maior que", um limite inferior exato 100(1 - α)% da taxa é dado por:
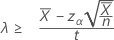
Se você especificar um valor de "comprimento", o limite inferior exato de 100 (1-α)% da média é dada por:
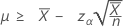
-
Se você especificar uma hipótese alternativa "menor que", um limite superior exato 100(1 - α)% da taxa é dado por:
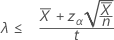
Se você especificar um valor de "comprimento", o limite superior exato de 100 (1-α)% da média é dada por:
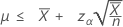
Notação
| Termo | Descrição |
|---|---|
| s | o número médio de ocorrências total no processo de Poisson |
| t | "comprimento" da observação |
| λ | valor verdadeiro da taxa para a população |
| μ | valor verdadeiro da média da população |
| Zx | o ponto percentil superior x da distribuição normal padrão, em que 0 < x < 1. |
| α | o nível alfa para o intervalo de confiança 100(1 – α)% |
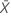 | número médio de ocorrências na amostra |
| n | tamanho amostral |
