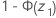Neste tópico
- Intervalo de confiança exato de Blaker ajustado e métodos de teste
- Método do intervalo de confiança exato de Clopper-Pearson
- Teste que corresponde ao intervalo de confiança exato de Clopper-Pearson
- Método do intervalo de confiança do escore de Wilson
- Teste de pontuação
- Intervalo de confiança de Agresti-Coull e métodos de teste
- Intervalo de confiança para aproximação normal de Wald
Intervalo de confiança exato de Blaker ajustado e métodos de teste
A configuração de análise para a hipótese alternativa especifica se deve produzir um intervalo de confiança bilateral ou um limite de confiança unilateral. Para uma hipótese alternativa de menor ou maior que a, a análise produz um limite de confiança unilateral. Para um limite de confiança unilateral, a análise usa o método exato de Clopper-Pearson.
Para uma hipótese alternativa bilateral, a análise produz um intervalo de confiança bilateral. A análise no Minitab Statistical Software produz o intervalo de confiança e o valor de p usando o algoritmo de Klaschka e Reiczigel.1 O nome desse método é o método exato Blaker ajustado. Este algoritmo numérico é mais rápido de calcular e produz intervalos de confiança e testes que concordam em geral. Os intervalos de confiança de Blaker ajustados também são exatos e aninhados.
O método exato de Blaker ajustado produz intervalos de confiança bicaudais para a proporção de eventos e produz valores de p para a hipótese alternativa de p ≠ p0. Blaker23 fornece um intervalo de confiança exato e bilateral invertendo a função de valor de p de um teste exato. Os intervalos de Clopper-Pearson são mais amplos e sempre contêm os intervalos de confiança de Blaker. Os intervalos do método exato de Blaker são aninhados. Essa propriedade significa que intervalos de confiança com níveis de confiança mais altos contêm intervalos de confiança com níveis de confiança mais baixos. Por exemplo, um intervalo de confiança Blaker 95% exato e bilateral contém o intervalo de confiança correspondente de 90%.
O algoritmo que o Minitab Statistical Software usa supera 2 limitações do método exato original de Blaker. Uma limitação é que o algoritmo numérico para calcular os intervalos de confiança é lento, principalmente quando o tamanho da amostra é grande. Outra limitação é que, para alguns dados, o método exato de Blaker original produz um intervalo que cobre uma proporção hipotética quando o valor de p é menor que o nível de significância que corresponde ao nível de confiança. A limitação também surge quando o intervalo de confiança não contém uma proporção hipotética quando o valor de p é maior que o nível de significância que corresponde ao nível de confiança.
Método do intervalo de confiança exato de Clopper-Pearson
O intervalo (PL, PU) é um intervalo de confiança bilateral, 100(1 – α)% de p. Quando a amostra não tem eventos, o limite inferior é 0. Quando a amostra tem apenas eventos, o limite superior é 1.
Limite inferior (unilateral)
Fórmula

Notação
| Termo | Descrição |
|---|---|
B(1 −  ; a, b) ; a, b) | inferior, 1 -  percentil da distribuição beta com parâmetros a e b percentil da distribuição beta com parâmetros a e b |
| x | número de eventos |
| n | número de ensaios |
Limite superior unilateral
Fórmula

Notação
| Termo | Descrição |
|---|---|
B( ; a, b) ; a, b) | Superior,  percentil da distribuição beta com parâmetros a e b percentil da distribuição beta com parâmetros a e b |
| x | número de eventos |
| n | número de ensaios |
Limite inferior (bilateral)
Observação
Limites bilateral para o método Clopper-Pearson estão disponíveis apenas pela linha de comando.
Fórmula
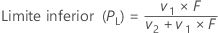
Notação
| Termo | Descrição |
|---|---|
| v1 | 2x |
| v2 | 2(n – x + 1) |
| x | número de eventos |
| n | número de ensaios |
| F | ponto α/2 inferior da distribuição F com v1 e v2 graus de liberdade |
Limite superior (bilateral)
Observação
Limites bilateral para o método Clopper-Pearson estão disponíveis apenas pela linha de comando.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| v1 | 2(x + 1) |
| v2 | 2(n – x) |
| x | número de eventos |
| n | número de ensaios |
| F | ponto α/2 superior da distribuição F com v1 e v2 graus de liberdade |
Teste que corresponde ao intervalo de confiança exato de Clopper-Pearson
Fórmula
- Ha: p ≠ p0
- p-valor =
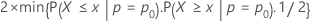
- Ha: p > p0
- p-valor = P{ X ≥ x | p = po}
- Ha: p < p0
- p-valor = P{ X ≤ x | p = po}
Notação
| Termo | Descrição |
|---|---|
| p0 | proporção hipotética |
| n | número de ensaios |
| p | probabilidade de um evento |
| x | número de eventos |
Método do intervalo de confiança do escore de Wilson
Wilson4 inverte o teste de pontuação para obter intervalos de confiança que o Minitab Statistical Software nomeia intervalos de confiança de Wilson-score. Os intervalos do escore de Wilson têm duas formas, uma sem correção de continuidade e outra com correção de continuidade. A cobertura dos intervalos sem a correção às vezes fica abaixo do nível de confiança nominal. O nível de confiança real dos intervalos com a correção é pelo menos o nível de confiança nominal. Para ambos os métodos, quando a amostra não tem eventos, o limite inferior é 0. Quando a amostra tem apenas eventos, o limite superior é 1.
Intervalos sem a correção de continuidade
O intervalo de confiança bilateral de 100(1 – α)% tem a seguinte fórmula:

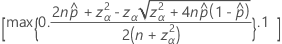
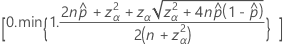
Intervalos com a correção de continuidade
O limite inferior do intervalo bilateral de 100(1 – α)% tem a seguinte fórmula:

O limite superior do intervalo bilateral de 100(1 – α)% tem a seguinte fórmula:
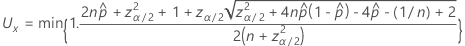
O limite inferior unilateral de 100(1 – α)% tem a seguinte fórmula:
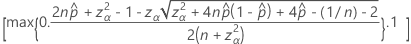
O limite superior unilateral de 100(1 – α)% tem a seguinte fórmula:
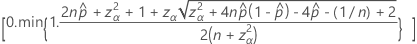
Notação
| Termo | Descrição |
|---|---|
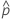 | probabilidade observada, 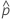 = x / n = x / n |
| x | número de eventos |
| n | número de ensaios |
| zγ | o ponto percentil superior da distribuição normal padrão em γ |
| α | 1 – nível de confiança/100 |
Teste de pontuação
Método sem a correção de continuidade
O teste que corresponde ao intervalo de confiança do escore de Wilson e ao método de aproximação normal (Web app) é o conhecido teste de pontuação. A estatística do teste de pontuação tem a seguinte equação:
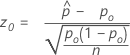
- Ha: p ≠ p0
- p-valor =
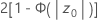
- Ha: p > p0
- p-valor =

- Ha: p < p0
- p-valor =

Método com a correção de continuidade
A estatística do teste e o valor de p para o procedimento com correção de continuidade dependem da hipótese alternativa.
- Ha: p ≠ p0
-
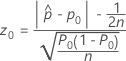
- Ha: p > p0
-
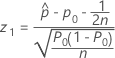
- Ha: p < p0
-
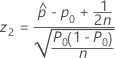
Notação
| Termo | Descrição |
|---|---|
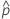 | probabilidade observada, x/n |
| x | número de eventos |
| n | número de ensaios |
| p0 | proporção hipotética |
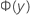 | função de distribuição cumulativa da distribuição normal padrão em y |
Intervalo de confiança de Agresti-Coull e métodos de teste
Intervalo de Confiança
Agresti e Coull5 fornecem um ajuste ao método de Wald para intervalos de confiança que melhora as propriedades de cobertura. Para um intervalo de confiança bicaudal de 95%, o ajuste adiciona aproximadamente 2 eventos e 2 não-eventos e, em seguida, calcula os intervalos de confiança a partir das fórmulas para as fórmulas do intervalo de confiança de Wald. Quando a amostra não tem eventos, o limite inferior é 0. Quando a amostra tem apenas eventos, o limite superior é 1.
O intervalo bilateral de 100(1 – α)% tem a seguinte fórmula:
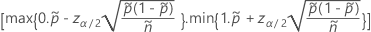
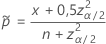
e
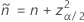
O limite inferior unilateral de 100(1 – α)% tem a seguinte fórmula:
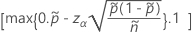
O limite superior unilateral de 100(1 – α)% tem a seguinte fórmula:

Para os limites unilaterais, use  na definição de
na definição de 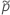 e
e 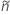 :
:
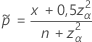
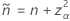
Teste que corresponde ao intervalo Agresti-Coull
A análise calcula o valor de p para o teste invertendo o procedimento de intervalo de confiança.
Notação
| Termo | Descrição |
|---|---|
| x | número de eventos |
| n | número de ensaios |
| zγ | o ponto percentil superior da distribuição normal padrão em γ |
| α | 1 – nível de confiança/100 |
Intervalo de confiança para aproximação normal de Wald
Fórmula
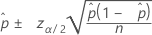
Notação
| Termo | Descrição |
|---|---|
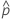 | probabilidade observada, 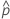 = x / n = x / n |
| x | número observado de eventos em n ensaios |
| n | número de ensaios |
| zα/2 | probabilidade acumulada inversa da distribuição normal padrão em 1 – α/2. |
| α | 1 – nível de confiança/100 |