Neste tópico
Método de Tukey para um modelo de efeitos mistos
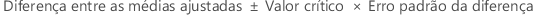
Para obter mais informações sobre como calcular as médias ajustadas e o erro padrão da diferença, acesse Métodos e fórmulas para médias ajustadas emAjustar modelo de efeitos mistos.
Observação
Os cálculos para a estatística de teste, valor-p ajustado, nível de confiança individual e tabela de informações de agrupamento correspondem aos cálculos para modelos lineares generalizados. Para obter mais informações, acesse os métodos e fórmulas para comparações de modelos lineares generalizados.
Valor crítico
| Termo | Descrição |
|---|---|
 | o 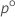 quantil da distribuição da amplitude estudentizada com df graus de liberdade |
 | a probabilidade simultânea de cometer um erro de Tipo I |
| m | o número de níveis no termo |
| df | os graus de liberdade |
Os graus de liberdade dependem se a comparação é para um termo de efeito fixo ou de um termo aleatório.
Graus de liberdade (df)
Para um termo de efeito fixo, os graus de liberdade (df) são os mesmos graus de liberdade para o ensaio do termo de efeito fixo correspondente. Para um termo aleatório, os graus de liberdade usam o método de aproximação de Satterthwaites.
Para obter mais informações sobre o cálculo dos graus de liberdade, acesse Métodos e fórmulas para testes de efeitos fixos em Ajustar modelo de efeitos mistos.
Método de Fisher para comparações pareadas em um modelo de efeitos mistos
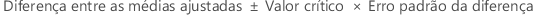
Para obter mais informações sobre como calcular as médias ajustadas e o erro padrão da diferença, acesse Métodos e fórmulas para médias ajustadas emAjustar modelo de efeitos mistos.
Observação
Os cálculos para a estatística de teste, valor-p ajustado, nível de confiança individual e tabela de informações de agrupamento correspondem aos cálculos para modelos lineares generalizados. Para obter mais informações, acesse os métodos e fórmulas para comparações de modelos lineares generalizados.
Valor crítico
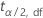
| Termo | Descrição |
|---|---|
 | o superior 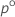 percentil da distribuição-t de Student com df graus de liberdade |
| α | a probabilidade individual de cometer um erro de Tipo I |
| df | os graus de liberdade |
Os graus de liberdade dependem se a comparação é para um termo de efeito fixo ou de um termo aleatório.
Graus de liberdade (df)
Para um termo de efeito fixo, os graus de liberdade (df) são os mesmos graus de liberdade para o ensaio do termo de efeito fixo correspondente. Para um termo aleatório, os graus de liberdade usam o método de aproximação de Satterthwaites.
Para obter mais informações sobre o cálculo dos graus de liberdade, acesse Métodos e fórmulas para testes de efeitos fixos em Ajustar modelo de efeitos mistos.
Método de Bonferroni para comparações pareadas em um modelo de efeitos mistos
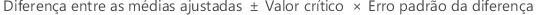
Para obter mais informações sobre como calcular as médias ajustadas e o erro padrão da diferença, acesse Métodos e fórmulas para médias ajustadas emAjustar modelo de efeitos mistos.
Observação
Os cálculos para a estatística de teste, valor-p ajustado, nível de confiança individual e tabela de informações de agrupamento correspondem aos cálculos para modelos lineares generalizados. Para obter mais informações, acesse os métodos e fórmulas para comparações de modelos lineares generalizados.
Valor crítico
| Termo | Descrição |
|---|---|
 | o superior 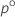 percentil da distribuição-t de Student com df graus de liberdade |
| α | a probabilidade simultânea de cometer um erro de Tipo I |
| c |  |
| k | o número de níveis no termo efeito fixo ou o termo aleatório |
| df | os graus de liberdade |
Os graus de liberdade dependem se a comparação é para um termo de efeito fixo ou de um termo aleatório.
Graus de liberdade (df)
Para um termo de efeito fixo, os graus de liberdade (df) são os mesmos graus de liberdade para o ensaio do termo de efeito fixo correspondente. Para um termo aleatório, os graus de liberdade usam o método de aproximação de Satterthwaites.
Para obter mais informações sobre o cálculo dos graus de liberdade, acesse Métodos e fórmulas para testes de efeitos fixos em Ajustar modelo de efeitos mistos.
Método de Sidak para comparações pareadas em um modelo de efeitos mistos
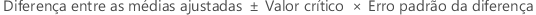
Para obter mais informações sobre como calcular as médias ajustadas e o erro padrão da diferença, acesse Métodos e fórmulas para médias ajustadas emAjustar modelo de efeitos mistos.
Observação
Os cálculos para a estatística de teste, valor-p ajustado, nível de confiança individual e tabela de informações de agrupamento correspondem aos cálculos para modelos lineares generalizados. Para obter mais informações, acesse os métodos e fórmulas para comparações de modelos lineares generalizados.
Valor crítico
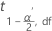
| Termo | Descrição |
|---|---|
 | o superior 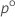 percentil da distribuição-t de Student com df graus de liberdade |
 |  |
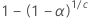| α | a probabilidade simultânea de cometer um erro de Tipo I |
| c |  |
| k | o número de níveis no termo efeito fixo ou o termo aleatório |
| df | os graus de liberdade |
Os graus de liberdade dependem se a comparação é para um termo de efeito fixo ou de um termo aleatório.
Graus de liberdade (df)
Para um termo de efeito fixo, os graus de liberdade (df) são os mesmos graus de liberdade para o ensaio do termo de efeito fixo correspondente. Para um termo aleatório, os graus de liberdade usam o método de aproximação de Satterthwaites.
Para obter mais informações sobre o cálculo dos graus de liberdade, acesse Métodos e fórmulas para testes de efeitos fixos em Ajustar modelo de efeitos mistos.
