Neste tópico
Tabela de informações de agrupamento para comparações pareadas
O Minitab utiliza os resultados do intervalo de confiança para a diferença entre duas médias de nível para obter as informações de agrupamento. As informações de agrupamento estão em uma matriz. Suponha que um termo tem k níveis, então, a dimensão máxima da matriz é o k x k. Se todos os níveis estiverem em um grupo, a dimensão é k x 1, com a letra "A" para todos os níveis de fator. Se todos os níveis estiverem em grupos diferentes, a dimensão é k x k com letras somente na diagonal.
- Ordene todas as médias dos quadrados mínimos em diferentes níveis de um termo em ordem decrescente, denotado como 1, 2, ... , k.
- Defina uma matriz k x k com o valor 0 em todas as células, onde k = número de níveis de fator.
- Para a coluna j, onde j = 1, ... , o Minitab faz o seguinte:
- Verifica os intervalos de confiança da média j - média r, onde r = j + 1, .. , k. Se o intervalo de r contiver 0, defina a ra linha e a ja célula de coluna, j) como 1.
- Configura a célula (j, j) como 1 se pelo menos uma célula na coluna j tiver valor 1.
- Calcula as somas das linhas da coluna 1 para a coluna j para a linha I = j + 1, ... , k. Se min (todas as somas de linha) >= 1, encerra o loop; senão, incrementa j em 1 e vai para o passo a.
- Para toda a linha i, o Minitab verifica a soma de todos os valores da coluna para a linha ≥ 1. Se a soma for zero, defina a célula da linha i e coluna j = 1, onde a coluna j é a primeira coluna na matriz com valores 0. Este processo produz uma matriz com os valores 1 e 0. O número total de grupos é o número de colunas diferentes de zero.
- Minitab corresponde as letras às colunas (por exemplo, A para Coluna 1, B para Coluna 2, etc.) e atribui as células com valor 1 à letra correta.
Tabela de informações de agrupamento para comparações múltiplas com um controle
O Minitab utiliza os resultados intervalo de confiança para a diferença entre cada média de nível e o nível de controle para obter as informações de agrupamento. As informações de agrupamento são em uma matriz com uma coluna.
O Minitab atribui a letra "A" para o nível de controle.
Se um intervalo contiver 0, então a média de nível está no mesmo grupo que o nível de controle. O Minitab atribui a letra "A" para a média de nível.
Se um intervalo não contiver 0, nenhuma letra é atribuída.
Método de Tukey
Fórmula
O método de Dunnett para comparações está disponível com um controle. A fórmula para intervalos de confiança é:
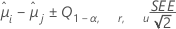
A fórmula para a estatística de teste é:


Para obter mais detalhes sobre o cálculo do valor-p ajustado, consulte as referências abaixo.
Para determinar a taxa de erro individual a partir da taxa de erro simultânea, utilize a seguinte fórmula:
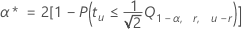
Notação
| Termo | Descrição |
|---|---|
 | as médias dos mínimos quadrados para o io nível de fator ou combinação de nível de fator |
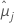 | as médias dos mínimos quadrados para o jo nível de fator ou combinação de nível de fator |
| r | o número de médias |
| Q1 − α, r, u | O 1 − α percentil da distribuição da faixa estudentizada para médias r, para comparar com u graus de liberdade |
| u | os graus de liberdade para erro a partir do modelo |
| SEE | o erro padrão da diferença estimativa entre as médias dos mínimos quadrados |
| α | a probabilidade simultânea de cometer um erro de Tipo I, baseado na distribuição da faixa estudentizada |
| α* | a probabilidade individual de cometer um erro Tipo I, baseado na distribuição de t para uma comparação |
Referências
1 Braun, H. I., editor (1994). The collected works of John W. Tukey: Volume VIII Multiple comparisons 1948-1983. New York: Chapman and Hall.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
Método Fisher
Fórmula
O Minitab oferece diferentes métodos de intervalo de confiança para comparar as médias dos tratamentos. Para o método de Fisher, os pontos de extremidade do intervalo de confiança e valores-p são os mesmos se as comparações forem pareadas ou com um controle. O método de Fisher usa o nível de confiança individual. A fórmula para intervalos de confiança é:
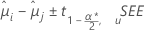
A fórmula para a estatística de teste é:

O valor p = 2*P{ T u > tu}
Para determinar o nível de confiança simultâneo partir da taxa de erro individual, utilize a seguinte fórmula:

Notação
| Termo | Descrição |
|---|---|
 | as médias dos mínimos quadrados para o io nível de fator ou combinação de nível de fator |
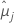 | as médias dos mínimos quadrados para o jo nível de fator ou combinação de nível de fator |
| t1-α*/2, u | O percentil superior α' /2 da distribuição t de Student com u graus de liberdade |
| Tu | Uma variável aleatória da distribuição t que tem u graus de liberdade para erro |
| Q | uma variável aleatória com a distribuição da taxa de estudentizados |
| α | a probabilidade simultânea de cometer um erro de Tipo I |
| α* | a probabilidade individual de cometer um erro Tipo I |
| u | os graus de liberdade para erro a partir do modelo |
| SEE | o erro padrão da diferença estimativa entre as médias dos mínimos quadrados |
Método Bonferroni
Fórmula
O Minitab oferece diferentes métodos de intervalo de confiança para comparar as médias dos tratamentos. Como o método de Bonferroni não faz suposições sobre a dependência entre as comparações, é o método mais conservador. "Conservador", neste contexto, indica que o verdadeiro nível de confiança provavelmente é maior do que o nível de confiança que está sendo exibido. A fórmula para intervalos de confiança é:
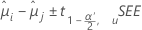
A fórmula para a estatística de teste é:

Notação
| Termo | Descrição |
|---|---|
 | as médias dos mínimos quadrados para o io nível de fator ou combinação de nível de fator |
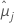 | as médias dos mínimos quadrados para o jo nível de fator ou combinação de nível de fator |
| t1-α*/2, u | O percentil superior α' /2 da distribuição t de Student com u graus de liberdade |
| α | a probabilidade simultânea de cometer um erro de Tipo I |
| α' | α / c |
| c | o número de comparações |
| u | os graus de liberdade para erro a partir do modelo |
| SEE | o erro padrão da diferença estimativa entre as médias dos mínimos quadrados |
O número de comparações depende se as comparações são pareadas ou com um controle. Seja k o número de médias que estão sendo comparadas. Os números de comparações estão na tabela abaixo.
| Pareadas | k (k – 1) / 2 |
| Com um controle | k – 1 |
Método Sidak
Fórmula
O Minitab oferece diferentes métodos de intervalo de confiança para comparar as médias dos tratamentos. O método de Sidak trata as comparações como se fossem independente, o que produz uma aproximação conservadora da taxa de erro verdadeiro. O método de Sidak é um pouco mais poderoso do que o método de Bonferroni.
A fórmula para intervalos de confiança é:
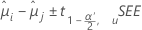
A fórmula para a estatística de teste é:

O valor-p ajustado = 1 − (1 − p)c.
Notação
| Termo | Descrição |
|---|---|
 | as médias dos mínimos quadrados para o io nível de fator ou combinação de nível de fator |
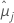 | as médias dos mínimos quadrados para o jo nível de fator ou combinação de nível de fator |
| t1-α*/2, u | O percentil superior α' /2 da distribuição t de Student com u graus de liberdade |
| α | a probabilidade simultânea de cometer um erro de Tipo I |
| α' | 1 – (1 – α ) 1/ k |
| u | os graus de liberdade para erro a partir do modelo |
| SEE | o erro padrão da diferença estimativa entre as médias dos mínimos quadrados |
| p | O valor-p não ajustado a partir da distribuição t para uma comparação |
| c | o número de comparações |
O número de comparações depende se as comparações são pareadas ou com um controle. Seja k o número de combinações de fatores. Os números de comparações estão na tabela abaixo.
| Pareadas | k (k – 1) / 2 |
| Com um controle | k – 1 |
Método de Dunnett
Fórmula
O Minitab oferece diferentes métodos de intervalo de confiança para comparar as médias dos tratamentos. O método de Dunnett para comparações está disponível com um controle. A fórmula para os intervalos de confiança é:

A fórmula para a estatística de teste é:

O valor-p ajustado é o resultado da integração da distribuição que Dunnett propõe para a estatística de teste. Para obter mais detalhes, consulte as referências abaixo.
Notação
| Termo | Descrição |
|---|---|
 | as médias dos mínimos quadrados para o io nível de fator ou combinação de nível de fator |
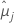 | as médias dos mínimos quadrados para o jo nível de fator ou combinação de nível de fator |
| D1-α, k-1, u | O percentil superior de α da distribuição que Dunnett propõe com comparações k − 1 e u de graus de liberdade |
| α | a probabilidade simultânea de cometer um erro de Tipo I |
| k | o número de médias para comparar |
| u | os graus de liberdade para erro a partir do modelo |
| SEE | o erro padrão da diferença estimativa entre as médias dos mínimos quadrados |
Referências
1 Dunnett, C. W. (January 01, 1955). A multiple comparison procedure for comparing several treatments with a control. Journal of the American Statistical Association, 50, 1096-1121.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
