O que são os componentes de nível e tendência para suavização exponencial dupla?

A suavização exponencial dupla usa um componente de nível, um componente de tendência e um componente sazonal em cada período. Ele usa dois pesos, ou parâmetros de suavização, para atualizar os componentes em cada período. As equações de suavização exponencial dupla são:

L_t = α Y_t + (1 - α) [L_t-1 + T_t-1]
T_t = γ[L_t - L_t-1] + (1 - γ) T_t-1
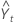= L_t-1 + T_t-1

onde L_t é o nível no tempo t, α é o peso para o nível, T_t é a tendência no tempo t, γ é o peso para a tendência, Y_t é o valor do dado no tempo t e 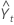é o ajustado, ou previsão para um período à frente, no tempo t.

A primeira observação é a número um, e as estimativas de nível e tendência devem ser inicialiadas para continuar. O método de inicialização usado para determinar como os valores suavizados serão obtidos em uma entre duas maneiras: com pesos gerados pelo o Minitab ou com pesos especificados.

Pesos ótimos ARIMA	Pesos especificados
O Minitab ajusta um modelo ARIMA (0, 2, 2) aos dados para minimizar a soma dos erros quadrados. Os componentes de tendência e nível são inicializados por previsão reversa.	O Minitab ajusta um modelo de regressão linear aos dados de séries temporais (vx y) versus tempo (vx x). A constante dessa regressão é a estimativa inicial do componente de nível, o coeficiente de inclinação é a estimativa inicial do componente de tendência.

Quando você especifica pesos que correspondem a um modelo ARIMA de raiz igual (0, 2, 2), o método de Holt passa para o método de Brown.