O Minitab oferece diversas análises que permitem analisar séries temporais. Essas análises incluem métodos simples para predição e suavização, métodos de análise de correlação e técnicas de modelagem ARIMA. Embora seja possível fazer análise de correlação separadamente da modelagem ARIMA, o Minitab apresenta os métodos de correlação como parte da modelagem ARIMA.
Métodos simples para predição e suavização
Os métodos simples para predição e suavização modelam os componentes em uma série geralmente fácil de se observar em um gráfico de séries temporais dos dados. Essa abordagem decompõe os dados em seus componentes e estende as estimativas dos componentes para o futuro para fornecer previsões. Você pode escolher entre métodos estáticos de análise de tendências e decomposição ou métodos dinâmicos de média móvel, suavização exponencial simples e dupla e o método de Winters. Os métodos estáticos possuem padrões que não mudam com o tempo; os métodos dinâmicos possuem padrões que mudam com o tempo e as estimativas são atualizadas usando valores vizinhos.
É possível usar dois métodos em combinação. Ou seja, você pode escolher um método estático para modelar um componente e um método dinâmico para modelar um outro componente. Por exemplo, você pode ajustar uma tendência estática usando análise de tendência e modelar dinamicamente o componente sazonal nos resíduos usando o método de Winters. Também é possível ajustar um modelo sazonal estático usando decomposição e modelar dinamicamente o componente de tendência nos resíduos usando suavização exponencial dupla. Também é possível aplicar uma análise de tendência e decomposição juntas para usar a seleção mais ampla de modelos de tendência usando a análise de tendências. Um adesvantagem de se combinar métodos é que os intervalos de confiança para previsões não são válidos.
A tabela a seguir fornece um sumário e um gráfico de ajustes e previsões de dados comuns para cada um dos métodos.
Análise de tendências
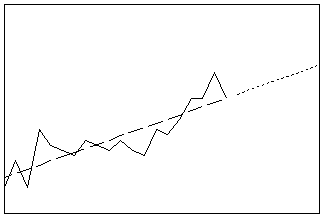
Ajusta um modelo de tendência a dados de séries temporais. Escolha entre modelos linear, quadrático, crescimento ou decrescimento exponencial, e de curva S de tendência. Use este procedimento para ajustar tendência quando não existem componentes sazonais na série.
- Comprimento: longo
- Perfil: extensão da linha de tendência
Decomposição
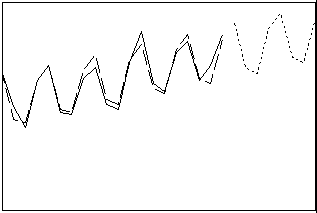
Separa a série temporal em componentes de tendência lineares, componentes sazonais e o erro. Escolha se o componente sazonal é aditivo ou multiplicativo com a tendência. Use este procedimento para prever quando existe um componente sazonal na série ou para examinar a natureza dos componentes.
- Comprimento: longo
- Perfil: tendência com padrão sazonal
Média móvel
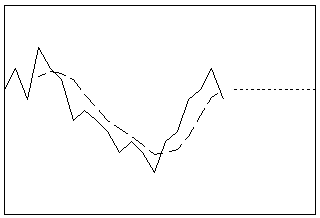
Suaviza os dados calculando a média de observações consecutivas em uma série. Você pode usar este procedimento quando os dados não possuem um componente de tendência. Se houver um componente sazonal, defina o comprimento da média móvel como igual ao comprimento do ciclo sazonal.
- Comprimento: curto
- Perfil: linha reta
Suavização de exponencial simples
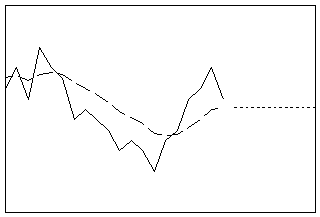
Suaviza os dados usando a fórmula de previsão ARIMA ótima de um passo adiante (0,1,1). Este procedimento funciona melhor sem conponentes sazonais ou de tendência. O único componente dinâmico em um modelo de média móvel é o nível.
- Comprimento: curto
- Perfil: linha reta
Suavização de exponencial dupla
Suaviza os dados usando a fórmula de previsão ARIMA ótima de um passo adiante (0,2,2). Este procedimento pode funcionar bem quando existe uma tendência, mas também serve como método geral para suavização. A Suavização Exponencial Dupla calcula estimativas dinâmicas para dois componentes: nível e tendência.
- Comprimento: curto
- Perfil: linha reta com inclinação igual à última estimativa de tendência
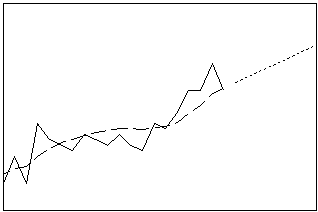
Método de Winter
Suaviza os dados por suavização exponencial de Holt-Winters. Use este procedimento quando existe tendência e sazonalidade, com esses dois componentes sendo aditivos ou multiplicativos. O método de Winters calcula estimativas dinâmicas dos três componentes: nível, tendência e sazonal.
- Comprimento: curto a médio
- Perfil: tendência com padrão sazonal
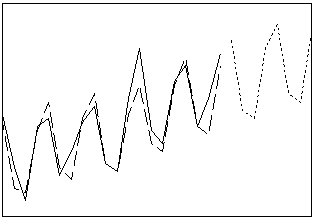
Análise de correlação e modelagem ARIMA
A modelagem ARIMA (média móvel integrada autorregressiva) também usa padrões nos dados, mas esses padrões podem não ser facilmente visíveis em um gráfico dos dados. A modelagem ARIMA usa diferenciação e as funções de autocorrelação e autocorrelação parcial para ajudar a identificar um modelo aceitável.
A modelagem ARIMA pode ser usada para modelar muitas séries temporais diferentes, com ou sem tendência ou componentes sazonais, e para fornecer previsões. O perfil da previsão depende do modelo ajustado. A vantagem da modelagem ARIMA em relação aos métodos de previsão simples e suavização é a maior flexibilidade no ajuste dos dados. Entretanto, identificar e ajustar um modelo pode demorar mais, e a modelagem ARIMA não é facilmente automatizada.
- Diferenças
- Calcula e armazena as diferenças entre valores de dados de uma série temporal. Se você quer ajustar um modelo ARIMA, mas seus dados têm uma tendência ou componente de sazonalidade, diferenciar os dados é um passo comum na avaliação de prováveis modelos ARIMA. A diferenciação é usada para simplificar a estrutura de correlação e para revelar qualquer padrão subjacente.
- Lag
- Calcula e armazena as defasagens de uma série temporal. Quando você defasa uma série temporal, o Minitab move os valores originais para baixo na coluna, e insere os valores ausentes na parte superior da coluna. O número de valores ausentes inseridos depende do comprimento da defasagem.
- Autocorrelação
- Calcula e cria um gráfico das autocorrelações de uma série temporal. A autocorrelação é a correlação entre observações de uma série temporal separada por unidades de tempo k. O gráfico de autocorrelações é chamado de função de autocorrelação (ACF). Visualize a ACF para conduzir sua escolha de termos a incluir em um modelo ARIMA.
- Autocorrelação parcial
- Calcula e cria um gráfico das autocorrelações parciais de uma série temporal. As autocorrelações parciais, como as autocorrelações, são correlações entre conjuntos de pares de dados ordenados de uma série temporal. Como ocorre com as correlações parciais no caso da regressão, as autocorrelações parciais medem a força da relação com outros termos que estão sendo explicados. A autocorrelação parcial em uma defasagem k é a correlação entre resíduos no tempo t de um modelo autorregressivo e observações em uma defasagem K com termos para todas as defasagens intervenientes no modelo autorregressivo. O gráfico de autocorrelações parciais é chamado de função de autocorrelação parcial (PACF). Visualize a PACF para conduzir sua escolha dos termos a incluir em um modelo ARIMA.
- Correlação cruzada
- Calcula e cria um gráfico das correlações entre duas séries temporais.
- ARIMA
- Ajusta um modelo ARIMA Box-Jenkins a uma série temporal. Em ARIMA, "Autorregressivo, "integrado" e "média móvel" consulte os passos de filtragem realizados no cálculo do modelo ARIMA até restar somente ruído aleatório. Use a ARIMA para modelar o comportamento das séries temporais e para gerar previsões.
