Suporte ao Minitab® 

Métodos e fórmulas para Método de Winters

Saiba mais sobre Minitab
Selecione o método ou a fórmula de sua escolha.

Neste tópico

Multiplicativo

Fórmula

O modelo multiplicativo é:

  • Lt = α (Yt / St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt / Lt) + (1 – δ) St–p
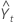  • = (Lt–1 + Tt–1) St–p

Notação

TermoDescrição
Ltnível no tempo t, α é o peso para o nível
Tttendência no tempo t,
γpeso para a tendência
Stcomponente sazonal no tempo t
δpeso do componente sazonal
pperíodo sazonal
Ytvalor do dado no tempo t
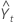valor ajustado, ou previsão para um período à frente, no tempo t

Método para calcular valores iniciais para nível e tendência para modelos multiplicativos

O método a seguir pressupõe um comprimento sazonal maior que 4.

  1. Encontre a média, o mínimo e o máximo dos dados. Para este exemplo:
    • Média: 554,208
    • Mín = 1
    • Máx = 1498,47
  2. Para cada linha de dados, calcule:
  3. Seja N igual ao comprimento sazonal. Para este exemplo, N = 12.
  4. Execute a regressão utilizando os primeiros “valores temporários” n (calculados na etapa 2) como variável Y, e um vetor de 1 a N como variável X. Então, para este exemplo:
    Y X
    4104,36 1
    4104,36 2
    4630,36 3
    4922,80 4
    4822,40 5
    5601,83 6
    4891,77 7
    4604,44 8
    4411,26 9
    4123,66 10
    4104,36 11
    4104,36 12

    A inclinação da linha de regressão é o valor inicial para a tendência.

  5. Ajuste a interceptação para a linha de regressão subtraindo:

A interceptação de seus dados é 4705,24. Subtraia 4103,36 da interceptação para obter uma interceptação ajustada de 601,879. Essa interceptação ajustada é o valor inicial para o nível.

Aditivo

Fórmula

O modelo aditivo é:
  • Lt = α (Yt – St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt – Lt) + (1 – δ) St–p
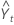  • = Lt–1 + Tt–1 + St–p

Notação

TermoDescrição
Ltnível no tempo t, α é o peso para o nível
Tttendência no tempo t,
γpeso para a tendência
Stcomponente sazonal no tempo t
δpeso do componente sazonal
pperíodo sazonal
Ytvalor do dado no tempo t
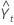valor ajustado, ou previsão para um período à frente, no tempo t

Método para calcular valores iniciais para nível e tendência para modelos aditivos

O método a seguir pressupõe um comprimento sazonal maior que 4.

  1. Seja N igual ao comprimento sazonal. Para este exemplo, N = 12.
  2. Execute a regressão usando os primeiros valores de dados N como variável Y, e um vetor de 1 a N como variável X. Então, para este exemplo:
    Y X
    1,00 1
    1,00 2
    527,00 3
    819,45 4
    719,04 5
    1498,47 6
    788,42 7
    501,08 8
    307,90 9
    20,30 10
    1,00 11
    1,00 12

    A inclinação da linha de regressão é o valor inicial para a tendência. A interceptação da linha de regressão é o valor inicial para o nível.

Método para calcular valores iniciais para índices sazonais para modelos aditivos

O método a seguir pressupõe um comprimento sazonal maior que 4.

  1. Execute a regressão utilizando os valores de dados como variável Y, e um vetor de 1 a 24 como variável X. Então, para este exemplo:
    Y X
    1,00 1
    1,00 2
    527,00 3
    819,45 4
    719,04 5
    1498,47 6
    788,42 7
    501,08 8
    307,90 9
    20,30 10
    1,00 11
    1,00 12
    83,00 13
    668,21 14
    1121,28 15
    1386,84 16
    1031,18 17
    988,60 18
    1380,30 19
    1005,97 20
    233,69 21
    211,87 22
    2,00 23
    2,40 24

    Use os resíduos deste modelo de regressão na próxima etapa

  2. Execute a regressão utilizando os resíduos como variável Y, e 12 variáveis indicadoras (z.1 a z.12) como as variáveis X. Ajuste o modelo de regressão sem um termo interceptador (constante). Então, para este exemplo:
    Resíduos z.1 z.2 z.3 z.4 z.5 z.6 z.7 z.8 z.9 z.10 z.11 z.12
    -508,261 1 0 0 0 0 0 0 0 0 0 0 0
    -512,170 0 1 0 0 0 0 0 0 0 0 0 0
    9,926 0 0 1 0 0 0 0 0 0 0 0 0
    298,460 0 0 0 1 0 0 0 0 0 0 0 0
    194,145 0 0 0 0 1 0 0 0 0 0 0 0
    969,667 0 0 0 0 0 1 0 0 0 0 0 0
    255,705 0 0 0 0 0 0 1 0 0 0 0 0
    -35,538 0 0 0 0 0 0 0 1 0 0 0 0
    -232,625 0 0 0 0 0 0 0 0 1 0 0 0
    -524,137 0 0 0 0 0 0 0 0 0 1 0 0
    -547,346 0 0 0 0 0 0 0 0 0 0 1 0
    -551,254 0 0 0 0 0 0 0 0 0 0 0 1
    -473,161 1 0 0 0 0 0 0 0 0 0 0 0
    108,141 0 1 0 0 0 0 0 0 0 0 0 0
    557,303 0 0 1 0 0 0 0 0 0 0 0 0
    818,952 0 0 0 1 0 0 0 0 0 0 0 0
    459,378 0 0 0 0 1 0 0 0 0 0 0 0
    412,890 0 0 0 0 0 1 0 0 0 0 0 0
    800,684 0 0 0 0 0 0 1 0 0 0 0 0
    422,451 0 0 0 0 0 0 0 1 0 0 0 0
    -353,739 0 0 0 0 0 0 0 0 1 0 0 0
    -379,468 0 0 0 0 0 0 0 0 0 1 0 0
    -593,247 0 0 0 0 0 0 0 0 0 0 1 0
    Os coeficientes deste modelo de regressão são os valores iniciais para os índices sazonais. Os coeficientes são:
    Período COEF1
    1 -490,711
    2 -202,014
    3 283,615
    4 558,706
    5 326,762
    6 691,278
    7 528,195
    8 193,456
    9 -293,182
    10 -451,803
    11 -570,297
    12 -574,005
    Observação

    As variáveis indicadoras z.1 a z.12 indicam a qual mês do período cada ponto de dados pertence. Por exemplo, a variável z.1 é igual a 1 para o primeiro mês do período, e é igual a 0 de outra forma.

Ajuste de modelo

O método de Winters usa um componente de nível, um componente de tendência e um componente sazonal em cada período. Ele usa três pesos, ou parâmetros de suavização, para atualizar os componentes em cada período. Os valores iniciais para os componentes de nível e tendência são obtidos de uma regressão linear no tempo. Os valores iniciais para o componente sazonal são obtidos de uma regressão de variável fictícia usando dados sem tendência.

Previsão

O método de Winters usa os componentes de nível, tendência e sazonais para gerar previsões. O método de Winters também usa os dados até o tempo da origem da previsão para gerar as previsões.

Fórmula

A previsão para m períodos à frente de um ponto t no tempo é:
  • Método multiplicativo: (Lt + mTt) * St + m −p
  • Método aditivo: Lt + mTt +St + m −p

Notação

TermoDescrição
Lt nível
Tt tendência no tempo t
TermoDescrição
St + m −pcomponente sazonal para o mesmo período do ano anterior

MAPE

O erro médio da porcentagem absoluta (MAPE) mede a precisão dos valores ajustados da série temporal. O MAPE expressa a precisão como porcentagem do erro.

Fórmula

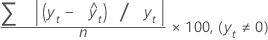
Notação

TermoDescrição
yt valor real no tempo t
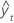valor ajustado
n número de observações

DAM

O desvio absoluto médio (DAM) mede a precisão dos valores ajustados da série temporal. O DAM expressa precisão nas mesmas unidades dos dados, o que ajuda a conceituar a magnitude do erro.

Fórmula

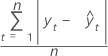
Notação

TermoDescrição
yt valor real no tempo t
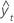valor ajustado
n número de observações

DQM

O desvio quadrado médio (DQM) é sempre calculado usando-se o mesmo denominador, n, independentemente do modelo. O DQM é uma medida mais sensível de uma previsão anormalmente maior do que o DAM.

Fórmula

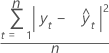
Notação

TermoDescrição
yt valor real no tempo t
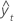valor ajustado
n número de observações
Copyright © 2025 Minitab, LLC. All rights Reserved.