Linear
Fórmula
O modelo de tendência linear é:
Yt = β0 + β1t + et
Notação
| Termo | Descrição |
|---|---|
| β0 | a constante |
| β1 | variação média de um período para o próximo |
| t | valor da unidade de tempo |
| et | o termo de erro |
Crescimento exponencial
Fórmula
O modelo de tendência de crescimento exponencial é responsável pelo crescimento ou o declínio exponencial. Por exemplo, uma conta de poupança pode exibir crescimento exponencial.
Yt = β0 * β1t * et
Notação
| Termo | Descrição |
|---|---|
| β0 | a constante |
| β1 | o coeficiente |
| t | valor da unidade de tempo |
| et | o termo de erro |
Quadrático
Fórmula
O modelo de tendência quadrático, que pode responder por curvatura simples nos dados, é:
Yt = β0 + β1t + β2t2 + et
Notação
| Termo | Descrição |
|---|---|
| β0 | a constante |
| β1 e β2 | os coeficientes |
| t | valor da unidade de tempo |
| et | o termo de erro |
Curva S
Fórmula
Os dados têm uma forma de S, os quais indicam qual direção da mudança varia ao longo do tempo.
Yt = 10a / (β0 + β1β2t)
Notação
| Termo | Descrição |
|---|---|
| β0 | a constante |
| β1 e β2 | os coeficientes |
| t | valor da unidade de tempo |
Pesos
Se você fornecer coeficientes de um ajuste de análise de tendência anterior, o Minitab realiza uma análise de tendência ponderada. Se o peso de um coeficiente específico for α, o Minitab estima o novo coeficiente com:
Fórmula
αp1 + (1 – α)p2
Notação
| Termo | Descrição |
|---|---|
| p1 | coeficiente estimado a partir dos dados atuais |
| p2 | coeficiente anterior |
Previsões
O Minitab usa a equação de tendência para calcular a previsão para valores de tempo específicos. Os dados anteriores à origem da previsão são usados para ajustar a tendência.
MAPE
O erro médio da porcentagem absoluta (MAPE) mede a precisão dos valores ajustados da série temporal. O MAPE expressa a precisão como porcentagem do erro.
Fórmula
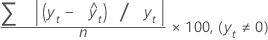
Notação
| Termo | Descrição |
|---|---|
| yt | valor real no tempo t |
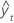 | valor ajustado |
| n | número de observações |
DAM
O desvio absoluto médio (DAM) mede a precisão dos valores ajustados da série temporal. O DAM expressa precisão nas mesmas unidades dos dados, o que ajuda a conceituar a magnitude do erro.
Fórmula
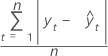
Notação
| Termo | Descrição |
|---|---|
| yt | valor real no tempo t |
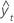 | valor ajustado |
| n | número de observações |
DQM
O desvio quadrado médio (DQM) é sempre calculado usando-se o mesmo denominador, n, independentemente do modelo. O DQM é uma medida mais sensível de uma previsão anormalmente maior do que o DAM.
Fórmula
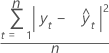
Notação
| Termo | Descrição |
|---|---|
| yt | valor real no tempo t |
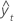 | valor ajustado |
| n | número de observações |
