Interprete os principais resultados para Previsão com o melhor modelo ARIMA

Complete as etapas a seguir para interpretar o processo de seleção do modelo e os resultados para a análise ARIMA. A saída-chave inclui as estatísticas de seleção de modelos, valor p, coeficientes, estatísticas qui-quadrado Ljung-Box e a função de autocorrelação dos resíduos.

Neste tópico

Passo 1: Considere modelos alternativos
Passo 2: Determinar se cada termo no modelo é significativo
Etapa 3: Determinar se o seu modelo atende à suposição da análise

Passo 1: Considere modelos alternativos

A tabela Seleção de Modelos exibe os critérios para cada modelo na pesquisa. A tabela exibe a ordem dos termos em que p é o termo autoregressivo, d é o termo diferente, e q é o termo médio móvel. Os termos sazonais usam letras maiúsculas e termos não sazonais que usam letras minúsculas.

Use o AIC, AICc e BIC para comparar modelos diferentes. É desejável que o resultado apresente valores menores. No entanto, o modelo com o menor valor para um conjunto de termos não necessariamente ajusta bem os dados. Além disso use os testes e os gráficos para avaliar se o modelo ajusta bem os dados. Por padrão, os resultados do ARIMA são para o modelo com o melhor valor de AICc.

Selecione Selecione o modelo alternativo para abrir uma caixa de diálogo que inclua a tabela Seleção de modelos. Compare os critérios para investigar modelos com desempenho semelhante.

Utilize a saída ARIMA para verificar se os termos do modelo são estatisticamente significativos e que o modelo atende aos pressupostos da análise. Se nenhum dos modelos na tabela se encaixar bem nos dados, considere modelos com diferentes ordens de diferenciamento.

Considere também um modelo alternativo quando um modelo alternativo funciona quase tão bem quanto o melhor modelo e tem pedidos mais baixos para os termos médios autoregressivos e móveis. Um modelo com menos termos é mais fácil de interpretar e pode ter melhor capacidade de previsão. Modelos com menos termos também são menos propensos a incluir termos redundantes. Por exemplo, termos de autoregressividade sazonal às vezes são redundantes com termos médios móveis sazonais. Termos redundantes às vezes tornam as estimativas dos coeficientes instáveis. Apresentamos a seguir algumas das consequências de coeficientes instáveis:

Os coeficientes podem parecer insignificantes mesmo quando existe uma relação significativa entre o preditor e a resposta.
Coeficientes para preditores altamente correlacionados variam fortemente de amostra para amostra.
A remoção de quaisquer termos altamente correlacionadas do modelo afetará significativamente os coeficientes estimados dos outros termos altamente correlacionados. Os coeficientes dos termos altamente correlacionadas pode até mesmo ter o sinal errado.

* AVISO * Modelos ARIMA (p, d, q) não-estimáveis que não incluem um termo constante:
(2; 1; 2)

Seleção de modelo

Modelo (d = 1)	Log-verossimilhança	AICc	AIC	BIC
p = 0; q = 2*	-197,052	400,878	400,103	404,769
p = 1; q = 2	-196,989	403,311	401,978	408,199
p = 1; q = 0	-201,327	407,029	406,654	409,765
p = 2; q = 0	-200,239	407,251	406,477	411,143
p = 1; q = 1	-200,440	407,655	406,880	411,546
p = 2; q = 1	-201,776	412,884	411,551	417,773
p = 0; q = 1	-204,584	413,542	413,167	416,278
p = 0; q = 0	-213,614	429,350	429,229	430,784

Principais resultados AICC, BIC e AIC

O ARIMA(0, 1, 2) tem o melhor valor do AICc. Os resultados da ARIMA a seguir são para o modelo ARIMA (0, 1, 2). Se o modelo não se encaixa bem nos dados, considere outros modelos com desempenho semelhante, como o modelo ARIMA(1, 1, 2) e o modelo ARIMA (1, 1, 1). Se nenhum dos modelos se encaixa bem nos dados, considere se deve usar um tipo diferente de modelo.

Passo 2: Determinar se cada termo no modelo é significativo

Para determinar se a associação entre a resposta e cada termo no modelo é estatisticamente significativa, compare o valor-p para o termo com o seu nível de significância a fim de avaliar a hipótese nula. A hipótese nula é de que o termo não seja significativamente diferente de 0, o que indica que não há associação entre a expressão e a resposta. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de concluir que o termo não é significativamente diferente de 0 quando for significativamente diferente de 0.

Valor-p ≤ α: O termo é estatisticamente significativo: Se o valor de p for menor ou igual ao nível de significância, é possível concluir que o coeficiente é estatisticamente significativo.
Valor-p > α: O termo não é estatisticamente significativo: Se o valor de p for maior do que o nível de significância, não é possível concluir que o coeficiente é estatisticamente significativo. Talvez seja necessário reajustar o modelo sem o termo.

Estimativas Finais de Parâmetros

Tipo	Coef.	EP de Coef	Valor-T	Valor-P
AR 1	-0,504	0,114	-4,42	0,000
Constante	150,415	0,325	463,34	0,000
Média	100,000	0,216

Principais resultados: P, Coef

O termo autorregressivo tem um valor-p menor do que o nível de significância de 0,05. É possível concluir que o coeficiente para o termo auto-regressivo é estatisticamente significativo e você deve manter o termo no modelo.

Etapa 3: Determinar se o seu modelo atende à suposição da análise

Use a estatística qui-quadrado de Ljung-Box e a função de autocorrelação dos resíduos para determinar se o modelo satisfaz aos pressupostos de que os resíduos são independentes. Se a suposição não for atendida, o modelo pode não se ajustar aos dados e você deve ter cautela ao interpretar os resultados.

Estatística qui-quadrado de Ljung-Box: Para determinar se os resíduos são independentes, compare o valor de p com o nível de significância para cada estatística qui-quadrado. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Se o valor de p for maior do que o nível de significância, é possível concluir que os resíduos são independentes e que o modelo atende à suposição.
Função de autocorrelação dos resíduos.: Se não houver correlações significativas presentes, é possível concluir que os resíduos são independentes. No entanto, é possível ver 1 ou 2 correlações significativas em lags de ordem superior que não são lags sazonais. Em geral, em vez disso, estas correlações são causadas por erro aleatório e não são um sinal de que a suposição não é atendida. Neste caso, é possível concluir que os resíduos são independentes.

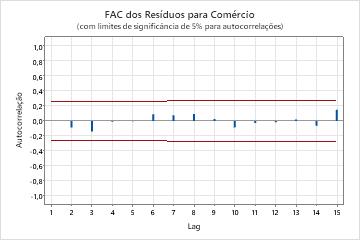
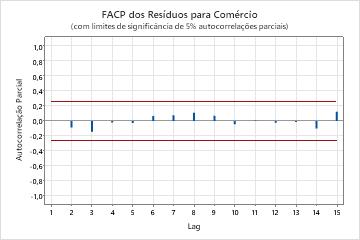
Principais resultados: valor de P, ACF de resíduos
Nestes resultados, os valores de p para a estatística qui-quadrado de Ljung-Box são maiores do que 0,05 e nenhuma das correlações para a função de autocorrelação dos resíduos são significativas. É possível concluir que o modelo atende à suposição de que os resíduos são independentes.

Lag	12	24	36	48
Qui-Quadrado	4,05	12,13	25,62	32,09
GL	10	22	34	46
Valor-P	0,945	0,955	0,849	0,940