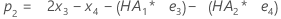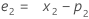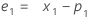Suporte ao Minitab® 

Métodos e fórmulas para Suavização exponencial dupla

Saiba mais sobre Minitab
Selecione o método ou a fórmula de sua escolha.

Neste tópico

Equação do modelo

A suavização exponencial dupla usa um componente de nível, um componente de tendência e um componente sazonal em cada período. A suavização exponencial dupla usa dois pesos, (também chamados de parâmetros de suavização), para atualizar os componentes em cada período. As equações de suavização exponencial dupla são as seguintes:

Fórmula

Lt= αYt+ (1 – α) [Lt–1 + Tt–1]

Tt= γ [Lt – Lt–1] + (1 – γ) Tt–1

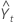= Lt−1 + Tt−1

Se a primeira observação é a número um, então as estimativas de nível e tendência devem ser inicializadas a fim de prosseguir. O método de inicialização usado para determinar como os valores suavizados serão obtidos em uma entre duas maneiras: com pesos ideais ou com pesos especificados.

Notação

TermoDescrição
Lt nível no tempo t
αpeso para o nível
Tt tendência no tempo t
γpeso para a tendência
Ytvalor do dado no tempo t
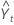valor predito para o tempo t.

Pesos

Pesos ótimos ARIMA

  1. O Minitab ajusta com um modelo ARIMA (0, 2, 2) os dados para minimizar a soma dos erros quadrados.
  2. Os componentes de tendência e nível são então inicializado pela previsão reversa.

Pesos especificados

  1. O Minitab ajusta um modelo de regressão linear aos dados de séries temporais (vx y) versus tempo (vx x).
  2. A constante dessa regressão é a estimativa inicial do componente de nível, o coeficiente de inclinação é a estimativa inicial do componente de tendência.

Quando você especifica pesos que correspondem a um modelo ARIMA de raiz igual (0, 2, 2), o método de Holt passa para o método de Brown1.

Método para calcular valores iniciais para nível e tendência

Estat > Séries temporais > Suavização de exp dupla pode armazenar estimativas de nível e tendência. O Minitab usa um dos seguintes métodos para calcular os valores na primeira linha dessas colunas, dependendo das opções especificadas na caixa de diálogo.

Se você escolher a opção ARIMA Ideal em Suavização de exp dupla, o Minitab usará o seguinte método para calcular os primeiros valores de nível e tendência. Você pode executar essas etapas à mão.

  1. Escolha Estat > Séries temporais > ARIMA para calcular os valores de peso ideais usando ARIMA. Preencha a caixa de diálogo como mostrado abaixo:
    1. Em Autorregressivo, insira 0.
    2. Em Diferença, insira 2.
    3. Em Média móvel, insira 2.
    4. Desmarque Incluir termo de constante no modelo.
    5. Clique em Armazenamento, e verifique Resíduos. Clique em OK em cada caixa de diálogo.
  2. O Minitab usa os valores de MA da saída ARIMA para calcular os pesos ideais da seguinte forma:

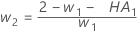
  3. Em seguida, o Minitab calcula de acordo com a observação inicial, usando dados de observações posteriores:
    onde:
    TermoDescrição
    pio valor previsto da i-ésima observação suavizada
    xio valor da i-ésima observação na série temporal
    eio valor do i-ésima residual, armazenado do ARIMA acima
  4. O Minitab calcula o valor inicial para nível (L1):

  5. O Minitab calcula o valor inicial para tendência (T1):

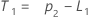
Se você especificar seus próprios pesos para nível e tendência Pesos para Usar na Suavização na caixa de diálogo Suavização de exp dupla, então o Minitab usará o seguinte método para calcular os valores iniciais para nível e tendência. Você pode executar essas etapas à mão.
  1. Crie uma coluna de índices de tempo igual ao comprimento da sua coluna de dados de séries temporárias. Uma coluna de inteiros de 1 a n é suficiente.
  2. Escolha Estat > Regressão > Regressão > Ajuste do modelo de regressão.
  3. Em Respostas, insira a coluna de dados de séries temporais. Em Preditores contínuos, insira a coluna de índices de tempo.
  4. Clique em Armazenamento, e verifique Coeficientes. Clique em OK em cada caixa de diálogo.
  5. O valor inicial do nível é:

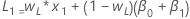
  6. O valor inicial da tendência é:

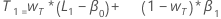    onde:
    TermoDescrição
    L1valor inicial do nível
    x1o valor da primeira observação na série temporal
    T1valor inicial para tendência
    wLo peso para nível
    wTo peso para tendência
    β0o coeficiente do termo da constante no modelo de regressão.
    β1o coeficiente para o termo preditor no modelo de regressão

Previsões

A suavização exponencial dupla usa os componentes de nível e tendência. A previsão para m períodos à frente de um ponto t no tempo da seguinte maneira:

Fórmula

Lt + mTt

Os dados até o tempo da origem da previsão são usados para a suavização.

Notação

TermoDescrição
Lt nível no tempo t
Tt tendência no tempo t

Limites de predição

Fórmula

Baseados no desvio absoluto médio (DAM). As fórmulas para os limites superiores e inferiores são as seguintes:
  • Limites superior = Previsão + 1,96 × dt × DAM
  • Limites inferior = Previsão – 1,96 × dt × DAM

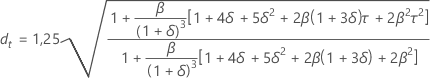
Notação

TermoDescrição
β max{α, γ)
δ1 – β
αconstante de suavização de nível
γconstante de suavização de tendência
τ
b0(T)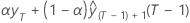
b1(T)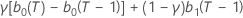

MAPE

O erro médio da porcentagem absoluta (MAPE) mede a precisão dos valores ajustados da série temporal. O MAPE expressa a precisão como porcentagem do erro.

Fórmula

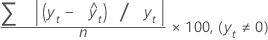
Notação

TermoDescrição
yt valor real no tempo t
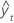valor ajustado
n número de observações

DAM

O desvio absoluto médio (DAM) mede a precisão dos valores ajustados da série temporal. O DAM expressa precisão nas mesmas unidades dos dados, o que ajuda a conceituar a magnitude do erro.

Fórmula

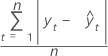
Notação

TermoDescrição
yt valor real no tempo t
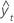valor ajustado
n número de observações

DQM

O desvio quadrado médio (DQM) é sempre calculado usando-se o mesmo denominador, n, independentemente do modelo. O DQM é uma medida mais sensível de uma previsão anormalmente maior do que o DAM.

Fórmula

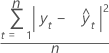
Notação

TermoDescrição
yt valor real no tempo t
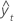valor ajustado
n número de observações
1 N.R.Farnum e L.W.Stanton (1989). Quantitative Forecasting Methods. PWS-Kent.
Copyright © 2025 Minitab, LLC. All rights Reserved.