Neste tópico
Duração
O número de observações na série temporal.
NMissing
Número de valores faltantes na série temporal.
Equação de tendências ajustadas
Use a equação tendência ajustada para calcular o componente de tendência para um período de tempo específico. A equação de tendência ajustada é uma representação algébrica da linha de tendência. A forma da equação de tendência ajustada é Yt = b0 + (b1 * t).
- yt é a variável
- b0 é a constante
- b1 é a inclinação
- t é o valor da unidade de tempo
O Minitab usa a equação de tendência ajustada e os índices sazonais para calcular os valores preditos.
Interpretação
Minitab utiliza a equação tendência ajustada para calcular a componente de tendência, que é utilizado em conjunto com os índices sazonais para calcular os valores preditos. Por exemplo, se a equação tendência ajustada for:
Yt = 173,06 + 2,111*t
O componente de tendência para o terceiro período é 173,06 + 2,11*3 = 182,45
O Minitab também calcula os dados sem divindindo-se os dados pelo componente de tendência (modelo multiplicativo) ou subtraindo o componente de tendência dos dados (modelo aditivo).
Índices sazonais e Sazonais
Os índices sazonais (também chamados Sazonais na tabela com os dados originais) são os efeitos sazonais no tempo t. O Minitab utiliza os índices sazonalmente para ajustar os dados, seja dividindo os dados com base nos índices sazonais (modelo multiplicativo) ou subtraindo os índices sazonais a partir dos dados (modelo aditivo). O Minitab também usa a equação de tendência ajustada e os índices sazonais para calcular os valores preditos.
MAPE
O erro médio absoluto percentual (MAPE) expressa precisão como uma porcentagem do erro. Como o MAPE é uma porcentagem, pode ser mais fácil de entender do que as outras estatísticas de medida de precisão. Por exemplo, se o MAPE é 5, em média, a previsão está incorreta em 5%.
No entanto, às vezes é possível observar um valor grande de MAPE mesmo que o modelo pareça ajustar bem os dados. Examine o gráfico para ver se todos os valores de dados estão próximos de 0. Como MAPE divide o erro absoluto pelos dados reais, valores próximos de 0 podem inflar em muito o MAPE.
Interpretação
Use para comparar os ajustes de diferentes modelos de séries temporais. Valores menores indicam um ajuste melhor. Se um único modelo não tem os valores mais baixos para todas as 3 medidas de precisão, em geral, o MAPE é a medida preferida.
As medidas de precisão são baseadas em resíduos de um período à frente. Em cada ponto no tempo, o modelo é usado para predizer o valor de Y para o próximo período no tempo. A diferença entre os valores preditos (ajustes) e o Y real são os resíduos de um período à frente. Por isso, as medidas de precisão fornecem uma indicação da precisão que pode ser esperada quando se prevê um período a partir do final dos dados. Portanto, eles não indicam a precisão da previsão de mais do que um período. Se você estiver usando o modelo de previsão, não deve basear sua decisão apenas nas medidas de precisão. Também deve examinar o ajuste do modelo para garantir que as previsões e o modelo seguem os dados de perto, especialmente no final da série.
MAD
O desvio absoluto médio (DAM) expressa precisão nas mesmas unidades dos dados, o que ajuda a conceituar a magnitude do erro. Outliers têm menor efeito sobre DAM do que sobre DMQ.
Interpretação
Use para comparar os ajustes de diferentes modelos de séries temporais. Valores menores indicam um ajuste melhor.
As medidas de precisão são baseadas em resíduos de um período à frente. Em cada ponto no tempo, o modelo é usado para predizer o valor de Y para o próximo período no tempo. A diferença entre os valores preditos (ajustes) e o Y real são os resíduos de um período à frente. Por isso, as medidas de precisão fornecem uma indicação da precisão que pode ser esperada quando se prevê um período a partir do final dos dados. Portanto, eles não indicam a precisão da previsão de mais do que um período. Se você estiver usando o modelo de previsão, não deve basear sua decisão apenas nas medidas de precisão. Também deve examinar o ajuste do modelo para garantir que as previsões e o modelo seguem os dados de perto, especialmente no final da série.
DMQ
O desvio médio quadrático (DMQ) mede a precisão dos valores de séries temporais ajustadas. Os outliers têm um efeito maior sobre o DMQ do que sobre o DAM.
Interpretação
Use para comparar os ajustes de diferentes modelos de séries temporais. Valores menores indicam um ajuste melhor.
As medidas de precisão são baseadas em resíduos de um período à frente. Em cada ponto no tempo, o modelo é usado para predizer o valor de Y para o próximo período no tempo. A diferença entre os valores preditos (ajustes) e o Y real são os resíduos de um período à frente. Por isso, as medidas de precisão fornecem uma indicação da precisão que pode ser esperada quando se prevê um período a partir do final dos dados. Portanto, eles não indicam a precisão da previsão de mais do que um período. Se você estiver usando o modelo de previsão, não deve basear sua decisão apenas nas medidas de precisão. Também deve examinar o ajuste do modelo para garantir que as previsões e o modelo seguem os dados de perto, especialmente no final da série.
Tendência
Os valores de tendência são os componentes de tendência que são calculados pela equação de tendência ajustada.
Interpretação
O componente de tendência para um período de tempo específico é calculado inserindo os valores de tempo específicos para cada observação no conjunto de dados na equação tendência ajustada. Por exemplo, se a equação de tendência ajustada é Yt = 5 + 10*t, o valor de tendência no tempo de 2, é 25 (25 = 5 + 10(2)).
Sem tendência
Valores sem tendência são dados com o componente de tendência removido. Os valores sem tendência são as diferenças entre os valores observados e os valores de tendência (modelo aditivo) ou a razão entre os valores observados e os valores de tendência (modelo multiplicativo).
Dessazonalização
Os valores de dessazonalização são dados com o componente sazonal removido. Os valores de dessazonalização são as diferenças entre os valores observados e os valores sazonais (modelo aditivo) ou os valores observados divididos pelos valores sazonais (modelo multiplicativo).
Predizer
Os valores preditos também são chamados ajustes. Os valores preditos são estimativas pontuais da variável no tempo (t).
As observações que têm valores preditos muito diferentes do valor observado pode ser anormais ou influente. Tente identificar a causa de todos os outliers. Corrija todos os erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
Erro
Os valores de erro também são chamados resíduos. Os valores de erro são as diferenças entre os valores observados e os valores previstos.
Interpretação
Represente graficamente os valores de erro para determinar se seu modelo é adequado. Os valores podem fornecer informações úteis sobre o quão bem o modelo ajusta os dados. Em geral, os valores de erro devem ser distribuídos aleatoriamente em torno de 0 sem nenhum padrão óbvio e não há valores anormais.
Período
O Minitab exibe o período quando você gera previsões. O período é a unidade de tempo da previsão. Por padrão, as previsões começam no final dos dados.
Previsão
As previsões são os valores ajustados obtidos a partir do modelo de série temporal. O Minitab exibe o número de previsões especificadas por você. As previsões começam tanto no final dos dados como no ponto de origem que você especificar.
Interpretação
Use previsões para predizer uma variável por um período de tempo especificado. Por exemplo, o gerente de um almoxarifado pode modelar a quantidade de produtos a ser encomendada para os próximos 3 meses com base nos pedidos dos últimos 60 meses.
A decomposição usa uma linha de tendência fixa e índices de sazonalidade fixos. Como a tendência e os índices sazonais são fixos, a decomposição deve ser utilizada somente para prever quando a tendência e a sazonalidade forem muito consistentes. É especialmente importante garantir que os ajustes correspondam aos valores reais no final das séries temporais. Se o padrão sazonal ou tendência não corresponderem aos ajustes no final dos dados, use Método de Winters.
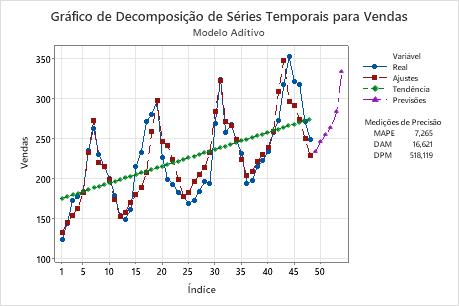
Neste gráfico, o modelo reverte a previsão dos dados no final das séries. Isto indica que a tendência ou padrão sazonal não são consistentes. Se você quiser prever esses dados, deve tentar o método de Winters para determinar se ele fornece um ajuste melhor para os dados.
Gráfico decomposição de séries temporais
O gráfico mostra as observações em função do tempo. O gráfico inclui a linha de tendência, os ajustes que são calculados a partir da tendência e componentes sazonais, as previsões e as medidas de precisão.
Interpretação
- Se o modelo ajustar os dados, você pode realizar Método de Winters e comparar os dois modelos.
- A decomposição usa uma tendência linear constante. Se a tendência parece ter curvatura, a decomposição não irá fornecer um bom ajuste. Você deve usar Método de Winters.
- Se o modelo não ajustar os dados, examine o gráfico para uma falta de sazonalidade. Se não houver nenhum padrão sazonal, você deve usar uma análise de séries temporais diferente. Para obter mais informações, acesse Quais análises de séries temporais devo usar?.

Neste gráfico, os ajuste acompanham os dados de perto, o que indica que o modelo ajusta os dados.
Análise de componente
- Dados originais
- Um gráfico de séries temporais dos dados originais
- Dados sem tendência
- Valores sem tendência são dados com o componente de tendência removido. Os valores sem tendência são as diferenças entre os valores observados e os valores de tendência (modelo aditivo) ou a razão entre os valores observados divididos pelos valores de tendência (modelo multiplicativo). Se o gráfico dos dados sem tendência parecem diferentes a partir dos dados originais, é possível concluir que existe um componente de tendência nos dados.
- Dados ajustados sazonalmente
- Valores sazonalmente ajustados são os dados com o componente sazonal removidos. Os valores sazonalmente ajustados são as diferenças entre os valores observados e os valores sazonais (modelo aditivo) ou os valores observados divididos pelos valores sazonais (modelo multiplicativo). Se o gráfico dos dados sazonalmente ajustados parecem diferentes a partir dos dados originais, é possível concluir que existe um componente sazonal nos dados.
- Seas. Adj. e Detr. Dados
- Os valores ajustados sazonalmente e valores sem tendência também são chamados de resíduos. Os resíduos são as diferenças entre os valores observados e os valores preditos. Examine o gráfico para determinar se o seu modelo é adequado. Os resíduos devem ser distribuídos aleatoriamente, sem padrões óbvios e nenhum valor incomum.
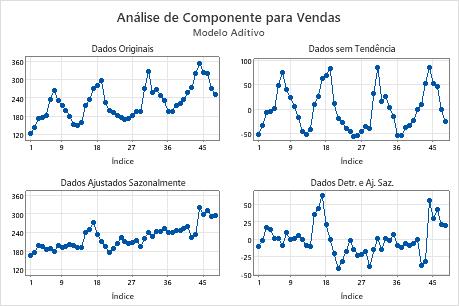
Neste gráfico, os dados sem tendência e os dados de sazonalidade ajustada parecem diferentes das observações originais. É possível concluir que um componente de tendência e existe um componente sazonal nos dados. As grandes resíduos positivos próximo ao fim dos dados indicam que o modelo reverte a previsão desses períodos de tempo.
Análise sazonal
- Índices sazonais
- Os índices sazonais são os efeitos sazonais no tempo. Use o gráfico para determinar a direção do efeito sazonal.
- Dados sem tendência por sazonalidade
- Os dados sem tendência são os dados com o componente de tendência removido. Use os boxplots para determinar qual o período sazonal tem a maior ou menor variação.
- Porcentagem da variação por sazonalidade
- O gráfico mostra a porcentagem de variação de cada sazonalidade. Use o gráfico para quantificar a variação de cada período sazonal.
- Resíduos por sazonalidade
- Os resíduos são as diferenças entre os valores observados e os valores preditos. Use o gráfico para determinar se há um efeito sazonal nos resíduos.
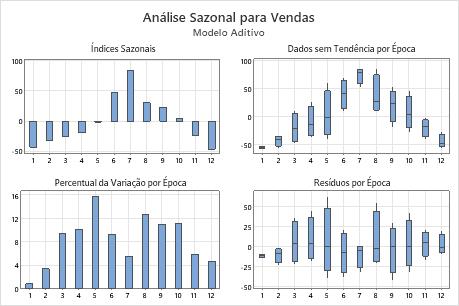
Neste gráfico, os índices sazonais indicam movimentos descendentes médios nos primeiros 5 meses e os 2 últimos meses da sazonalidade e movimentos ascendentes médios do 6º ao 10º mês. O gráfico de variação percentual por sazonalidade mostra que o 1º mês tem a menor variação e o 5º mês tem a maior variação. Os boxplots dos dados sem tendência por sazonalidade mostram que os meses em que o valor absoluto do efeito sazonal é grande tendem a ter uma menor variação do que meses em que o efeito sazonal é menor. O gráfico de resíduos por sazonalidade não mostra nenhum efeito óbvio da sazonalidade sobre os resíduos.
Histograma dos resíduos
O histograma dos resíduos mostra a distribuição dos resíduos para todas as observações. Se o modelo adaptar bem os dados, os resíduos devem ser aleatórios com média de 0. Assim, o histograma deve ser aproximadamente simétrico em torno de 0.
Gráficos de probabilidade normal dos resíduos
Um gráfico normal dos resíduos mostra os resíduos versus seus valores esperados quando a distribuição é normal.
Interpretação
Use um gráfico normal de resíduos para determinar se os resíduos são normalmente distribuídos. No entanto, esta análise não necessita de resíduos normalmente distribuídos.
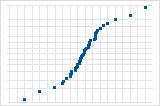
A curva S sugere uma distribuição com caudas longas.
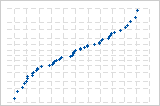
A curva S invertida sugere uma distribuição com caudas curtas.
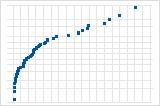
A curva descendente implica uma distribuição assimétrica à direita.
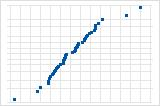
Alguns pontos situados longe da linha sugerem uma distribuição com outliers.
Resíduos versus ajustes
O gráfico de resíduos versus ajustes mostra os resíduos no eixo Y e os valores ajustados no eixo X.
Interpretação
Use gráfico de resíduos versus valores ajustados para determinar se os resíduos são não-viciados e têm uma variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Curvilíneo | Um termo de ordem mais alta ausente |
| Um ponto que está distante de zero | Um outlier |
Se você observar variância ou padrões inconstantes nos resíduos, as previsões podem não ser precisas.
Resíduos x ordem
O gráfico de resíduos versus ordem mostra os resíduos na ordem em que os dados foram coletados.
Interpretação
Use o gráfico de resíduos versus ordem para determinar o quão preciso são os ajustes em comparação com os valores observados durante o período de observação. Os padrões nos pontos podem indicar que o modelo não ajusta os dados. De maneira ideal, os resíduos no gráfico devem cair aleatoriamente em torno da linha central.
| Padrão | O que o padrão pode indicar |
|---|---|
| A tendência consistente de longo prazo | O modelo não ajusta os dados |
| Uma tendência de curto prazo | Um deslocamento ou uma mudança no padrão |
| Um ponto que está longe de os outros pontos | Um outlier |
| Um deslocamento repentina nos pontos | O padrão subjacente para os dados mudou |
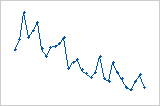
Os resíduos sistematicamente diminuem conforme a ordem das observações aumentam da esquerda para a direita.
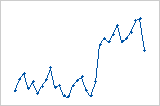
Uma mudança repentina nos valores dos resíduos ocorre de baixo (esquerda) para alto (direita).
Resíduos em função de variáveis
O gráfico de resíduos em função de variáveis apresenta os resíduos comparados com outras variáveis
Interpretação
Use o gráfico para determinar se a variável afeta a resposta de uma forma sistemática. Se os padrões estiverem presentes nos resíduos, as outras variáveis estão associadas à resposta. É possível usar essas informações como base para estudos adicionais.
