Lag
O lag é o número de períodos de tempo que separa duas séries temporais. O número padrão de lags varia de (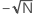
+ 10) até (
+ 10).
Função de correlação cruzada (CCF)
A função de correlação cruzada é a correlação entre as observações de duas séries temporais xt e yt, separadas por k unidades de tempo (a correlação entre yt+k e xt).
Interpretação
Use a função de correlação cruzada para determinar se existe uma relação entre duas séries temporais. Para determinar se existe uma relação entre as duas séries, procure por um grande correlação, com as correlações em ambos os lados que rapidamente se tornam não significativas. Em geral, a correlação é significativa quando o valor absoluto é maior do que 
, onde n é o número de observações e k é o lag. Este cálculo é uma regra de ouro em termos de procedimento com base em aproximação normal de amostra grande. Se a correlação cruzada da população de lag k for zero para k = 1, 2, ... então, para n razoavelmente grande, rxy(k) será aproximadamente distribuído normalmente, com média (μ) zero e desvio padrão (σ) 1/
. Como aproximadamente 95% de uma população normal estão a 2 desvios padrão da média, um teste que rejeite a hipótese de que a correlação cruzada da população de lag k é igual a zero, quando | rxy(k) | é maior que 2/
possui um nível de significância (α) de aproximadamente 5%.
Observação
A interpretação para a função de correlação cruzada depende da hipótese de que não há autocorrelação. Para obter mais informações, acesse Procure por evidências de autocorrelação.
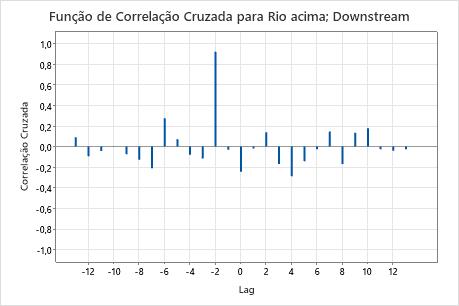
Neste gráfico, a correlação no lag -2 é de aproximadamente 0,92. Como 0,92 > 0,5547 = 
a correlação é significativa. É possível concluir que a água se move a partir da localização a montante para o local a jusante em dois dias.
