Um analista coletou dados sobre o número de passageiros de companhias aéreas por 108 meses. O analista quer usar um modelo ARIMA para gerar previsões para os dados. Em um enredo de séries tempoariais, o analista vê que a diferença entre os picos sazonais altos e baixos cresce ao longo do tempo. Este padrão indica que a variância não está estacionária. O analista realiza uma transformação Box-Cox para tornar a variância estacionária antes que o analista se encaixe no modelo ARIMA.
- Abra os dados amostrais PassageirosAereos.MWX.
- Escolha .
- Em Séries, digite Número de passageiros.
- Em Período sazonal, insira 12.
- Selecione λ ótimo para que o Minitab Statistical Software procure uma transformação para usar.
- Em Coluna de estampa para escala de tempo, digite Data.
- Em Armazenar séries transformadas em, digite Transformado. Clique em OK.
Interprete os resultados
A tabela Método mostra as configurações para a análise e o valor de λ para a transformação.
Nesses resultados, o período sazonal é de 12 e a análise busca um valor λ entre a faixa padrão de -1 e 2. O valor ideal para λ é aproximadamente -0,14. A análise arredonda o valor para 0 e usa a transformação natural do log.
Método
| Período sazonal | 12 |
|---|---|
| Selecione λ ideal do intervalo | [-1; 2] |
| λ ótimo | -0,144439 |
| λ ideal arredondado | 0 |
| Série transformada = ln(Número de passageiros) |
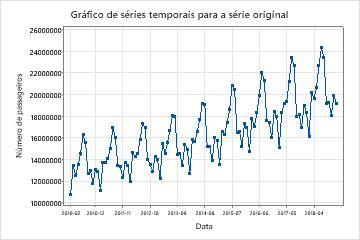
Compare a série temporal da série original com o gráfico da série temporal da série transformada para verificar se a transformação torna a variância estacionária.
Nestes resultados, o gráfico da série original mostra a variância não estacionária. Nesses dados, a diferença entre os pontos altos e baixos em um ciclo sazonal aumenta à medida que o tempo passa. Este padrão mostra que a variância aumenta à medida que o tempo passa.
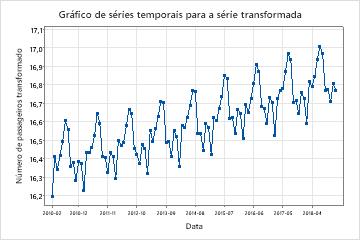
Examine o gráfico da série temporais da série transformada para verificar se a transformação torna a variância estacionária.
Nesses resultados, o gráfico da série temporais da série transformada mostra uma diferença aproximadamente uniforme entre os pontos altos e baixos nos ciclos sazonais. Esse padrão mostra que a transformação torna a variância estacionária.
Examine também o gráfico da série temporais dos dados transformados para avaliar outras características importantes da série transformada. Por exemplo, as suposições para um modelo ARIMA incluem que a série tem uma média estacionária, além de uma variância estacionária. Se um enredo da série transformada mostra que a série transformada não tem uma média estacionária, tente Teste de Dickey-Fuller aumentado ver se a diferença dos dados torna a média da série estacionária.
Nesses resultados, a série transformada mostra uma tendência de alta. Este padrão mostra que a média da série não está estacionária. Use a Teste de Dickey-Fuller aumentado coluna armazenada de dados transformados para determinar se a diferença torna a série estacionária.