Passo 1: Determine se os dados estão estacionários ou estacionários
A tabela de teste Dickey-Fuller aumentada fornece as hipóteses, uma estatística de teste, um valor p e uma recomendação sobre se considerar diferentes sazonais para tornar os dados estacionários.
A estatística do teste fornece uma maneira de avaliar a hipótese nula. As estatísticas de teste inferiores ou iguais ao valor crítico fornecem evidências contra a hipótese nula.
O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.
Para determinar se deve fazer diferença nos dados, compare a estatística de teste com o valor crítico ou o valor p ao seu nível de significância. Como o valor p contém mais aproximação, a recomendação da análise utiliza o valor crítico para avaliar a hipótese nula quando o nível de significância é de 0,01, 0,05 ou 0,10. Normalmente, a conclusão é a mesma para o valor crítico e o valor p. A hipótese nula é que os dados não são estacionários, o que implica que a diferença é um passo razoável para tentar tornar os dados estacionários.
- Nível de significância ≤ de valor P
- Estatística de teste ≤ valor crítico
- Se o valor p for menor ou igual ao nível de significância ou se a estatística de teste for menor ou igual ao valor crítico, a decisão é rejeitar a hipótese nula. Como os dados fornecem evidências de que os dados estão parados, a recomendação da análise é proceder sem divergências.
- Nível de significância> de valor P
- Estatística de teste> valor crítico
- Se o valor p for maior que o nível de significância ou se a estatística de teste for maior que o valor crítico, a decisão é não rejeitar a hipótese nula. Como os dados não fornecem evidências de que os dados estão parados, a recomendação do analyis é determinar se a diferença torna a média dos dados estacionária.
Se os dados estiverem parados, o teste não recomenda diferenciar. Explorar modelos ARIMA que não incluam termos diferentes. Se os dados não estiverem estacionários, então explore os modelos ARIMA que incluem termos diferentes. Use o gráfico de série temporal dos dados diferenciados para ver se as diferenças entre observações consecutivas são um conjunto estacionário de dados. Se os dados diferenciados estiverem parados, então os modelos ARIMA com um termo de primeira ordem para diferenciação são razoáveis de considerar.
Nestes resultados, a estatística de teste de 2,29045 é maior que o valor crítico de aproximadamente -2,96053. Como os resultados não rejeitam a hipótese nula de que os dados não são estacionários, a recomendação do teste é considerar a diferença para tornar os dados estacionários.
Teste de Dickey-Fuller aumentado
| Hipótese nula: | Os dados são não-estacionários |
|---|---|
| Hipótese alternativa: | Os dados são estacionários |
| Estatística de teste | Valor-p | Recomendação |
|---|---|---|
| 2,29045 | 0,999 | Estatística de teste > valor crítico de -2,96053. |
| Nível de significâncial = 0,05 | ||
| Não rejeitou a hipótese nula. | ||
| Considere diferenciação para tornar os dados estacionários. |
Passo 2: Examine o efeito de diferenciar os dados
Quando a conclusão do teste for diferente, examine as parcelas dos dados diferenciados para características de dados que não estão estacionários. Uma tendência na trama da série temporal é um exemplo de um padrão que indica que a média dos dados não está estacionária. Na parcela ACF, grandes picos que diminuem lentamente também indicam dados que não estão parados. Se você ver esses padrões nos dados diferentes, então considere se deve encaixar um modelo ARIMA com uma segunda ordem de diferenciação. Normalmente, 1 ou 2 pedidos de diferenciamento são suficientes para fornecer um ajuste razoável aos dados.
Se os dados diferentes estiverem parados, então uma abordagem razoável é incluir uma única ordem de diferenciamento não sazonal em um modelo ARIMA. Para obter mais informações sobre modelos ARIMA, acesse Visão geral de ARIMA.
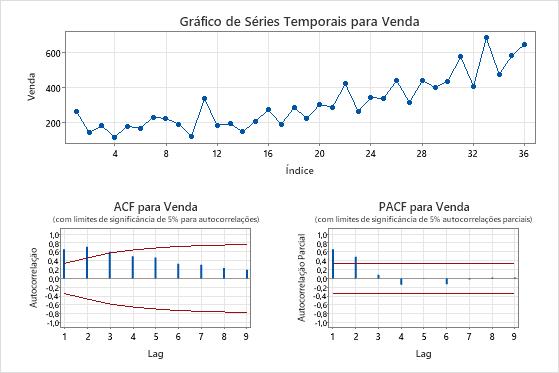
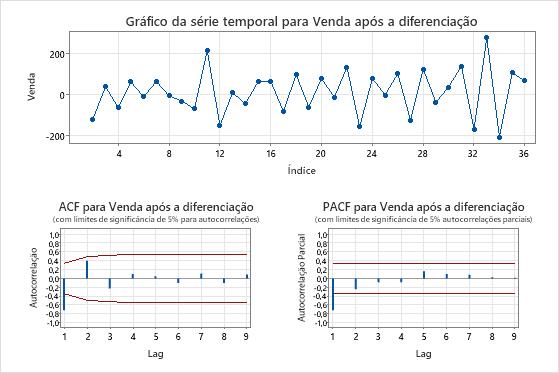
As tramas da série time mostram o resultado da diferença. Nesses resultados, o enredo da série temporal dos dados originais mostra uma tendência clara. O enredo da série temporal dos dados diferenciados mostra as diferenças entre valores consecutivos. Os dados diferenciados aparecem estacionários porque os pontos seguem um caminho horizontal sem padrões óbvios na variação.
As gráficos ACF também mostram o efeito da diferença. Nestes resultados, o gráfico ACF dos dados originais mostra picos lentamente reduzidos entre os atrasos. Este padrão indica que os dados não estão parados. Na gráfico ACF dos dados diferenciados, o único pico que é significativamente diferente de 0 é o lag 1.
Nestes resultados, as gráfico da série temporal e as gráficos da ACF confirmam os resultados do teste. Portanto, uma abordagem razoável é a diferença dos dados e, em seguida, encaixar um modelo médio autoregressivo e móvel para fazer previsões.