Neste tópico
Tabela de métodos
A tabela Método mostra as configurações para a análise e a ordem de lag selecionada.
Nesses resultados, a ordem máxima de defasagem que a análise avalia é 9. A análise utiliza o modelo com a maior ordem de lag de 4 para calcular os resultados do teste.
Método
| Ordem máxima de lag para termos no modelo de regressão | 9 |
|---|---|
| Critério para selecionar ordem de lag | AIC mínimo |
| Termos adicionais | Constante |
| Ordem de lag selecionada | 4 |
| Linhas usadas | 36 |
Tabela de teste Dickey-Fuller aumentado
A tabela de teste Dickey-Fuller aumentado fornece as hipóteses, uma estatística de teste, um valor p e uma recomendação sobre se considerar diferente para tornar a série estacionária.
A estatística do teste fornece uma maneira de avaliar a hipótese nula. As estatísticas de teste inferiores ou iguais ao valor crítico fornecem evidências contra a hipótese nula.
O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.
Para determinar se deve fazer diferença nos dados, compare a estatística de teste com o valor crítico ou o valor p ao seu nível de significância. Como o valor p contém mais aproximação, a recomendação da análise utiliza o valor crítico para avaliar a hipótese nula quando o nível de significância é de 0,01, 0,05 ou 0,10. Normalmente, a conclusão é a mesma para o valor crítico e o valor p. A hipótese nula é que os dados não são estacionários, o que implica que a diferença é um passo razoável para tentar tornar os dados estacionários.
- Nível de significância ≤ de valor P
- Estatística de teste ≤ valor crítico
- Se o valor p for menor ou igual ao nível de significância ou se a estatística de teste for menor ou igual ao valor crítico, a decisão é rejeitar a hipótese nula. Como os dados fornecem evidências de que os dados estão parados, a recomendação da análise é proceder sem divergências.
- Nível de significância> de valor P
- Estatística de teste> valor crítico
- Se o valor p for maior que o nível de significância ou se a estatística de teste for maior que o valor crítico, a decisão é não rejeitar a hipótese nula. Como os dados não fornecem evidências de que os dados estão parados, a recomendação do analyis é determinar se a diferença torna a média dos dados estacionária.
Nestes resultados, a estatística de teste de 2,29045 é maior que o valor crítico de aproximadamente -2,96053. Como os resultados não rejeitam a hipótese nula de que os dados não são estacionários, a recomendação do teste é considerar a diferença para tornar os dados estacionários.
Teste de Dickey-Fuller aumentado
| Hipótese nula: | Os dados são não-estacionários |
|---|---|
| Hipótese alternativa: | Os dados são estacionários |
| Estatística de teste | Valor-p | Recomendação |
|---|---|---|
| 2,29045 | 0,999 | Estatística de teste > valor crítico de -2,96053. |
| Nível de significâncial = 0,05 | ||
| Não rejeitou a hipótese nula. | ||
| Considere diferenciação para tornar os dados estacionários. |
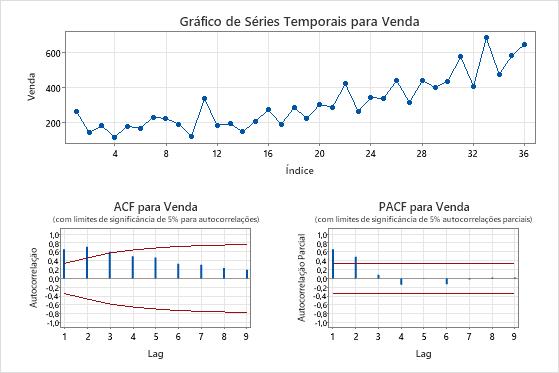
Gráficos da série original
- Gráfico de séries temporais
- Use o gráfico da série original para examinar as características dos dados originais. Uma tendência é um exemplo de um padrão que indica uma média não estacionária. Use a diferença para tentar tornar a média estacionária.
- Gráfico ACF
- Use a função de correção automática (ACF) a partir dos dados originais para procurar um padrão que indique que a média dos dados não está estacionária. Um padrão comum são grandes picos através de lags que morrem muito lentamente.
- Gráfico PACF
- Normalmente, você usa a função de autocorrelação parcial (PACF) de dados estacionários para procurar padrões que indiquem a presença de termos autoregressivos em um modelo ARIMA. Se os dados originais não estiverem estacionários, use o enredo PACF da série diferente para procurar termos de candidato para o modelo ARIMA.
Nesses resultados, os dados mostram uma tendência crescente na trama da série temporal. A primeira defasagem na trama da ACF mostra um grande pico que excede o limite de significância de 5%, depois diminui muito lentamente. Esses padrões indicam que a média dos dados não está estacionária.
Como as vendas não têm relação com um preditor que explicaria uma tendência determinística e o analista quer usar um modelo ARIMA para prever as vendas, diferir os dados é uma maneira razoável de tentar tornar a média da série estacionária.
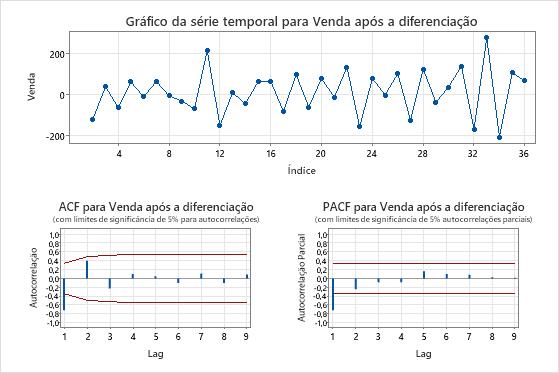
Gráficos da série diferente
- Gráfico da série time após diferenciamento
- Use o gráfico de série temporal dos dados diferenciados para verificar se a diferença torna a média dos dados estacionária. O enredo da série temporal mostra as diferenças entre observações consecutivas. Dados com uma média estacionária seguem um caminho horizontal na gráfico da série temporais.
- Gráfico ACF e gráfico PACF após diferenciamento
- Use o ACF dos dados diferenciados para verificar se a diferença torna a média dos dados estacionária. Gráficos com picos que diminuem rapidamente são características de dados estacionários.
Nesses resultados, o enredo da série temporais mostra que a média e a variância dos dados diferenciados são aproximadamente constantes. Os dados parecem estar parados.
Na gráfico ACF dos dados diferenciados, o único pico que é significativamente diferente de 0 é o lag 1. Esse padrão também sugere que os dados estão parados.