Neste tópico
Coeficientes
Os coeficientes são estimados utilizando um algoritmo iterativo que calcula estimativas de mínimos quadrados. A cada iteração, as previsões retroativas são calculadas e o SSE é calculado. Para obter mais detalhes, consulte Box e Jenkins1.
O algoritmo ARIMA é baseado na rotina de ajuste do pacote TSERIES elaborado pelo Professor William Q. Meeker, Jr., da Iowa State University2. Agradecemos ao Professor Meeker por sua ajuda na adaptação de sua rotina ao Minitab.
Previsões retroativas
As previsões retroativas são calculados usando o modelo especificado e as estimativas dos parâmetros da iteração atual. Para obter mais detalhes, consulte Cryer3.
SSE
Fórmula

Notação
| Termo | Descrição |
|---|---|
| n | número de observações total |
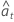 | resíduos utilizando as estimativas dos parâmetros da iteração, incluindo previsões de volta |
SS para resíduos
Fórmula
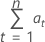
Notação
| Termo | Descrição |
|---|---|
| n | número de observações total |
| at | resíduos utilizando as estimativas dos parâmetros finais, excluindo as previsões de volta |
DF para resíduos
Fórmula
Para um modelo com termo constante:
(n – d) – p – q – 1
Para um modelo sem termo constante:
(n – d) – p – q
Notação
| Termo | Descrição |
|---|---|
| n | número de observações total |
| d | número de diferenças |
| p | número de parâmetros auto-regressivos incluídos no modelo |
| q | número de parâmetros de médias móveis incluídos no modelo |
MS para resíduos
Fórmula
SS / DF
Estatística qui-quadrado
Fórmula
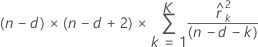
Notação
| Termo | Descrição |
|---|---|
| n | número de observações total |
| d | número de diferenças |
| K | 12, 24, 36, 48 |
| k | lag |
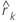 | autocorrelação dos resíduos para o ko lag |
DF para estatística qui-quadrado
Fórmula
Para um modelo com termo constante:
K – p – q – 1
Para um modelo sem termo constante:
K – p – q
Notação
| Termo | Descrição |
|---|---|
| K | 12, 24, 36, 48 |
| p | número de parâmetros auto-regressivos incluídos no modelo |
| q | número de parâmetros de médias móveis incluídos no modelo |
Valor de p para estatística qui-quadrado
Fórmula
P(X < χ2)
Notação
| Termo | Descrição |
|---|---|
| X | distribuído como χ2(DF) |
Previsões
Fórmula
As previsões são calculadas de forma recursiva, com base no modelo e nas estimativas dos parâmetros. Por exemplo, se um modelo ARIMA é ajustado com um termo autorregressivo (AR (1)) e um termo de diferenciação sazonal com um período sazonal de 12, este modelo é ajustado:
Yt – Yt–12 = γ + Φ(Yt–1 – Yt–12–1)
Para estimar  , a primeira previsão, em que k é a origem, encontre:
, a primeira previsão, em que k é a origem, encontre:
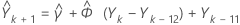
Assim, você encontra 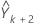 , da mesma maneira, e assim por diante.
, da mesma maneira, e assim por diante.
Para calcular o intervalo de predição de 95% para a previsão, primeiro você deve calcular os pesos.
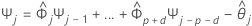
em que 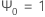 ,
,  para j < 0, e
para j < 0, e  para j > q.
para j > q.
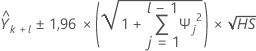
Notação
| Termo | Descrição |
|---|---|
| Yt | valor real no tempo t |
| Φ | termo autorregressivo |
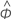 | termo autorregressivo estimado |
| γ | termo constante |
| d | número de diferenças |
| p | número de parâmetros autorregressivos |
| q | número de parâmetros da média móvel |
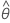 | termo da média móvel estimado |
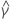 | termo constante estimado |
| QM | quadrado médio do erro |
