Neste tópico
Etapa 1: Determine se cada termo no modelo é significativo
- Valor de p ≤ α: o termo é estatisticamente significativo
- Se o valor de p for menor ou igual ao nível de significância, é possível concluir que o coeficiente é estatisticamente significativo.
- Valor de p > α: o termo não é estatisticamente significativo
- Se o valor de p for maior do que o nível de significância, não é possível concluir que o coeficiente é estatisticamente significativo. Talvez seja necessário reajustar o modelo sem o termo.
Estimativas Finais de Parâmetros
| Tipo | Coef. | EP de Coef | Valor-T | Valor-P |
|---|---|---|---|---|
| AR 1 | -0,504 | 0,114 | -4,42 | 0,000 |
| Constante | 150,415 | 0,325 | 463,34 | 0,000 |
| Média | 100,000 | 0,216 |
Principais resultados: P, Coef
O termo auto-regressivo tem um valor de p que é menor do que o nível de significância de 0,05. É possível concluir que o coeficiente para o termo auto-regressivo é estatisticamente significativo e você deve manter o termo no modelo.
Etapa 2: Determine quão bem o modelo se ajusta aos dados
Use o quadrado médio do erro (MS) para determinar o quão bem o modelo ajusta os dados. Os valores menores indicam um modelo de ajuste melhor.
Somas Residuais dos Quadrados
| GL | SQ | QM |
|---|---|---|
| 58 | 366,733 | 6,32299 |
Principais resultados: MS
O quadrado médio do erro é 6,323 para este modelo. Este valor não é muito informativo, por si só, mas você pode usá-lo para comparar os ajustes de diferentes modelos ARIMA.
Etapa 3: Determinar se o seu modelo atende à suposição da análise
- Estatística qui-quadrado de Ljung-Box
- Para determinar se os resíduos são independentes, compare o valor de p com o nível de significância para cada estatística qui-quadrado. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Se o valor de p for maior do que o nível de significância, é possível concluir que os resíduos são independentes e que o modelo atende à suposição.
- Função de autocorrelação dos resíduos.
- Se não houver correlações significativas presentes, é possível concluir que os resíduos são independentes. No entanto, é possível ver 1 ou 2 correlações significativas em lags de ordem superior que não são lags sazonais. Em geral, em vez disso, estas correlações são causadas por erro aleatório e não são um sinal de que a suposição não é atendida. Neste caso, é possível concluir que os resíduos são independentes.
Estatística Qui-Quadrado de Box-Pierce (Ljung-Box) Modificada
| Lag | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| Qui-Quadrado | 4,05 | 12,13 | 25,62 | 32,09 |
| GL | 10 | 22 | 34 | 46 |
| Valor-P | 0,945 | 0,955 | 0,849 | 0,940 |
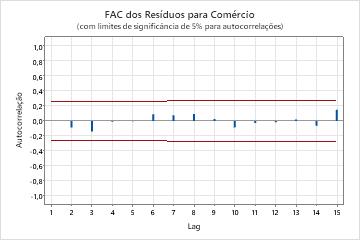
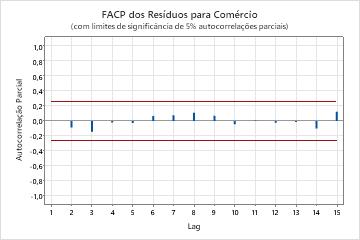
Principais resultados: valor de P, ACF de resíduos
Nestes resultados, os valores de p para a estatística qui-quadrado de Ljung-Box são maiores do que 0,05 e nenhuma das correlações para a função de autocorrelação dos resíduos são significativas. É possível concluir que o modelo atende à suposição de que os resíduos são independentes.
