Neste tópico
Gráfico de séries temporais
O gráfico da série temporal exibe os dados em ordem cronológica. Quando você gerar previsões, o Minitab exibe as previsões e os seus limites de confiança de 95% no gráfico.
Interpretação
- Determinar se diferentes há variações presentes nos dados. Se houver variações diferentes presentes, você deve transformar os dados para que a variância seja constante.
- Determine se os dados estão centralizados em torno de uma média constante. Se a média não for constante, talvez você precise diferenciar os dados para tornar a média constante.
ACF de resíduos
O gráfico mostra a função de autocorrelação dos resíduos. A função de autocorrelação é uma medida da correlação entre as observações de uma série temporal que são separadas por k unidades de tempo (yt e yt–k).
Interpretação
Use a função de autocorrelação dos resíduos para determinar se o modelo satisfaz aos pressupostos de que os resíduos são independentes. Se a suposição não for atendida, o modelo pode não se ajustar aos dados e você deve ter cautela ao interpretar os resultados. Se não houver correlações significativas presentes, é possível concluir que os resíduos são independentes. No entanto, é possível ver 1 ou 2 correlações significativas em lags de ordem superior que não são lags sazonais. Em geral, esses lags são devidos a erros aleatórios, e não são um sinal de que a suposição não é cumprida. Assim, neste caso, também é possível concluir que os resíduos são independentes.
PACF de resíduos
A função de autocorrelação parcial é uma medida da correlação entre as observações de uma série temporal que são separadas por k unidades de tempo (yt e yt–k), após o ajuste para a presença de todos os outros termos de menor lag (yt–1, yt–2, ..., yt–k–1).
Interpretação
Use a função de autocorrelação parcial dos resíduos para determinar se o modelo satisfaz aos pressupostos de que os resíduos são independentes. Se a suposição não for atendida, o modelo pode não se ajustar aos dados e você deve ter cautela ao interpretar os resultados. Se não houver correlações significativas presentes, é possível concluir que os resíduos são independentes.
Histograma dos resíduos
O histograma dos resíduos mostra a distribuição dos resíduos para todas as observações. Se o modelo adaptar bem os dados, os resíduos devem ser aleatórios com média de 0. Assim, o histograma deve ser aproximadamente simétrico em torno de 0.
Gráficos de probabilidade normal dos resíduos
Um gráfico normal dos resíduos mostra os resíduos versus seus valores esperados quando a distribuição é normal.
Interpretação
Use um gráfico normal de resíduos para determinar se os resíduos são normalmente distribuídos. No entanto, esta análise não necessita de resíduos normalmente distribuídos.
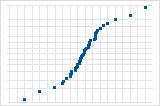
A curva S sugere uma distribuição com caudas longas.
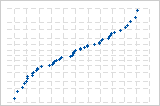
A curva S invertida sugere uma distribuição com caudas curtas.
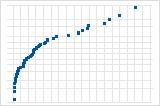
A curva descendente implica uma distribuição assimétrica à direita.
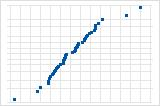
Alguns pontos situados longe da linha sugerem uma distribuição com outliers.
Resíduos versus ajustes
O gráfico de resíduos versus ajustes mostra os resíduos no eixo Y e os valores ajustados no eixo X.
Interpretação
Use gráfico de resíduos versus valores ajustados para determinar se os resíduos são não-viciados e têm uma variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Curvilíneo | Um termo de ordem mais alta ausente |
| Um ponto que está distante de zero | Um outlier |
Se você observar variância ou padrões inconstantes nos resíduos, as previsões podem não ser precisas.
Resíduos x ordem
O gráfico de resíduos versus ordem mostra os resíduos na ordem em que os dados foram coletados.
Interpretação
Use o gráfico de resíduos versus ordem para determinar o quão preciso são os ajustes em comparação com os valores observados durante o período de observação. Os padrões nos pontos podem indicar que o modelo não ajusta os dados. De maneira ideal, os resíduos no gráfico devem cair aleatoriamente em torno da linha central.
| Padrão | O que o padrão pode indicar |
|---|---|
| A tendência consistente de longo prazo | O modelo não ajusta os dados |
| Uma tendência de curto prazo | Um deslocamento ou uma mudança no padrão |
| Um ponto que está longe de os outros pontos | Um outlier |
| Um deslocamento repentina nos pontos | O padrão subjacente para os dados mudou |
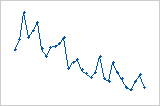
Os resíduos sistematicamente diminuem conforme a ordem das observações aumentam da esquerda para a direita.
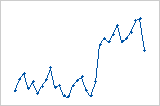
Uma mudança repentina nos valores dos resíduos ocorre de baixo (esquerda) para alto (direita).
Resíduos em função de variáveis
O gráfico de resíduos em função de variáveis apresenta os resíduos comparados com outras variáveis
Interpretação
Use o gráfico para determinar se a variável afeta a resposta de uma forma sistemática. Se os padrões estiverem presentes nos resíduos, as outras variáveis estão associadas à resposta. É possível usar essas informações como base para estudos adicionais.
