Usos da distribuição Weibull para modelar dados de confiabilidade
- Durante o período de envelhecimento acelerado, qual é a expectativa de falha dos itens em termos percentuais? Por exemplo, qual é a expectativa de falha para os fusíveis, em termos percentuais, durante o período de envelhecimento acelerado de oito horas?
- Quantas reivindicações de garantia podem ser esperadas durante a fase de vida útil? Por exemplo, quantos pedidos de garantia você espera receber durante a vida útil de 50.000 milhas deste pneu?
- Quando o desgaste rápido está previsto para ocorrer? Por exemplo, quando a manutenção regular deve ser programada para impedir que os motores entrem em sua fase de desgaste?
A distribuição Weibull pode modelar dados que são assimétricos à direita, esquerda ou simétrica. Portanto, a distribuição é usado para avaliar a confiabilidade em diversas aplicações, incluindo tubos de vácuo, capacitores, rolamentos de esferas, relés e resistências de materiais. A distribuição Weibull também pode modelar uma função de risco está diminuindo, aumentando ou permanece constante, permitindo que ela descreva qualquer fase da vida útil de um produto.
A distribuição Weibull pode não funciona com tanta eficiência para falhas de produtos causadas por reações químicas ou processos de degradação, como a corrosão, que podem ocorrer com as falhas de semicondutores. Normalmente, estes tipos de situações são modeladas usando a distribuição lognormal.
- Distribuição de Rayleigh
- Quando a distribuição de Weibull tem um parâmetro de forma de 2, ele é conhecido como distribuição de Rayleigh. Esta distribuição é frequentemente usada para descrever os dados de medição no campo da engenharia de comunicações, como medidas para a perda de retorno da entrada, a injeção de banda lateral de modulação, supressão de portadora, e desvanecimento de RF. Esta distribuição também é normalmente usada no teste de vida de dispositivos de eletrovácuo.
- Modelo do elo mais fraco
- A distribuição de Weibull também pode modelar uma distribuição de vida com muitos processos idênticos e independentes que levam a falhas e nos quais o primeiro componente a atingir um estágio crítico determina o tempo para falha. A teoria do valor extremo serve como base para ess emodelo do "elo mais fraco", onde muitas falhas competem pelo local da primeira falha. Como a distribuição de Weibull pode ser teoricamente derivada da distribuição de menor valor extremo, ela também pode fornecer um modelo eficaz para aplicações de elo mais fraco como falhas de capacitores, rolamentos, relés e resistência dos materiais. Entretanto, se a variável de interesse puder ter valores negativos, a distribuição de menor valor extremo é melhor porque a distribuição de Weibull só pode modelar valores positivos devido ao limite inferior de 0.
Exemplo 1: Capacitores
Os capacitores foram testados sob grande estresse para obter dados de falha (em horas). Os dados de falha foram modelados por uma distribuição Weibull.
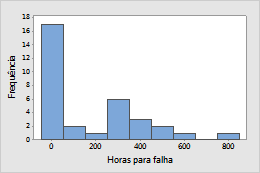
Exemplo 2: Filamentos
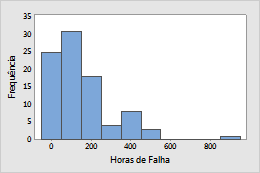
Uma empresa fabrica filamentos de lâmpadas incandescentes cujo desgaste não é esperado durante um longo período de uso normal. Os engenheiros na empresa desejam garantir as lâmpadas para 10 anos de operação. Os engenheiros estressam as lâmpadas para simular longos períodos de uso e registram as horas até a falha de cada lâmpada.
Relação entre parâmetros da distribuição Weibull, funções de confiabilidade e funções de risco
Você pode modelar as características de muitas distribuições de vida diferentes ajustando o parâmetro de forma, β, da distribuição de Weibull.
0 < ß < 1
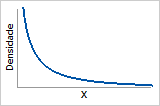
Função de densidade de probabilidade
Decrescendo exponencialmente do infinito
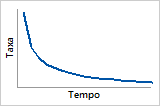
Função de perigo
Índice de falhas inicialmente alto que descresce ao longo do tempo (primeira parte da função de perigo em forma de banheira)
ß = 1
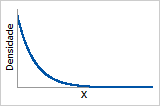
Função de densidade de probabilidade
decresce exponencialmente de 1/α (α = parâmetro de escala)

Função de perigo
Índice de falhas constante durante a vida do produto (segunda parte da função de perigo em forma de banheira)
ß = 1.5
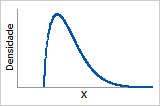
Função de densidade de probabilidade
Cresce até o pico e descresce
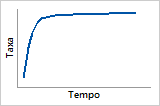
Função de perigo
Índice de falhas crescente com o maior aumento na primeira fase
ß = 2
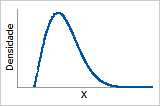
Função de densidade de probabilidade
Distribuição de Rayleigh
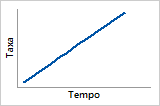
Função de perigo
Índice de falhas linearmente crescente
3 ≤ ß ≤4
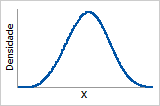
Função de densidade de probabilidade
Forma de sino
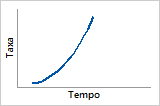
Função de perigo
Aumenta rapidamente
ß > 10
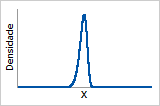
Função de densidade de probabilidade
Similar à distribuição de valor extremo
Função de perigo
Cresce muito rapidamente
