Engenheiros querem avaliar a confiabilidade de um invólucro de compressor reprojetado para motores a jato. Para testar o projeto, os engenheiros usam uma máquina para jogar um único projétil em cada invólucro de compressor. Após o impacto do projétil, engenheiros inspecionam o compressor a cada doze horas quanto a falha.
Os engenheiros realizam uma regressão com dados de vida para avaliar a relação entre o projeto do invólucro, o peso do projétil e o tempo de falha. Eles também querem estimar os tempos de falha no qual eles podem esperar que 1% e 5% dos motores falhem. Os engenheiros usam uma distribuição Weibull para modelar os dados.
- Abra os dados das amostras, ConfiabilidadeMotorJato.MWX.
- Selecione .
- Selecione As respostas são dados censurados arbitrariamente/não-censurados.
- Em Variáveis/variáveis iniciais, insira Início.
- Em Variáveis finais, insira Fim.
- Em Modelo, insira Experimento e Peso.
- Em Fatores (opcional), insira Experimento.
- Clique em Estimativa. Em Inserir valores da nova preditor, insira Novo ExperimentoNovo Pesos.
- Em Estimar percentis para percentuais, insira 1 5 e depois clique em OK.
- Clique em Gráficos. Selecione Gráfico de probabilidade para resíduos padronizados.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
Na tabela de regressão, os valores-p para o projeto e peso são significativos a um nível-α de 0,05. Portanto, os engenheiros concluíram que o projeto do invólucro e o peso do projétil exercem um efeito estatisticamente significativo sobre os tempos de falha. Os coeficientes para os preditores podem ser utilizados para definir uma equação que descreve a relação entre a o projeto do invólucro, o peso do projétil e o tempo de falha para os motores.
A tabela de percentis mostra os 1º e 5º percentis para cada combinação de projeto de invólucro e peso de projétil. O tempo que passa antes de 1% ou 5% dos motores falhar é mais longo para o novo projeto do invólucro do que o projeto de invólucro padrão, em todos os pesos de projéteis. Por exemplo, depois de ter sido submetido a um projétil de 10 libras, é possível esperar que 1% dos motores com um projeto de invólucro padrão falhe após aproximadamente 101,663 horas. Com o novo projeto de invólucro, é possível esperar a falha de 1% dos motores após aproximadamente 205,882 horas.
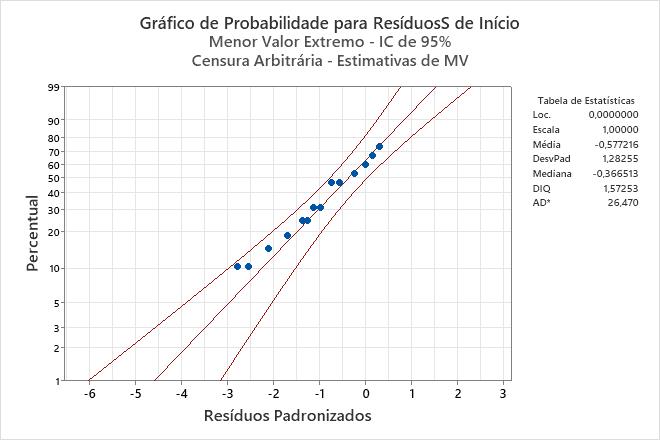
O gráfico de probabilidade dos resíduos padronizados mostra que os pontos seguem uma linha aproximadamente reta. Portanto, os engenheiros podem assumir que o modelo é apropriado.
Censura
| Informações de Censura | Contagem |
|---|---|
| Valor censurado à direita | 25 |
| Valor de censura do intervalo | 23 |
Tabela de Regressão
| IC Normal de 95,0% | ||||||
|---|---|---|---|---|---|---|
| Preditor | Coef. | Erro Padrão | Z | P | Inferior | Superior |
| Intercepto | 6,68731 | 0,193766 | 34,51 | 0,000 | 6,30754 | 7,06709 |
| Experimento | ||||||
| Padrão | -0,705643 | 0,0725597 | -9,72 | 0,000 | -0,847857 | -0,563428 |
| Peso | -0,0565899 | 0,0212396 | -2,66 | 0,008 | -0,0982187 | -0,0149611 |
| Forma | 5,79286 | 1,07980 | 4,02001 | 8,34755 | ||
Teste de Qualidade de Ajuste de Anderson-Darling (ajustado)
Tabela de Percentis
| IC Normal de 95,0% | ||||||
|---|---|---|---|---|---|---|
| Percentual | Experimento | Peso | Percentil | Erro Padrão | Inferior | Superior |
| 1 | Padrão | 5,0 | 134,911 | 17,6574 | 104,385 | 174,363 |
| 1 | Padrão | 7,5 | 117,113 | 16,0279 | 89,5591 | 153,144 |
| 1 | Padrão | 10,0 | 101,663 | 16,3830 | 74,1295 | 139,423 |
| 1 | Nova | 5,0 | 273,214 | 36,8022 | 209,819 | 355,763 |
| 1 | Nova | 7,5 | 237,171 | 32,6878 | 181,028 | 310,726 |
| 1 | Nova | 10,0 | 205,882 | 32,8675 | 150,568 | 281,518 |
| 5 | Padrão | 5,0 | 178,749 | 16,9676 | 148,404 | 215,300 |
| 5 | Padrão | 7,5 | 155,168 | 14,1107 | 129,836 | 185,443 |
| 5 | Padrão | 10,0 | 134,698 | 15,4568 | 107,568 | 168,670 |
| 5 | Nova | 5,0 | 361,994 | 36,0778 | 297,761 | 440,084 |
| 5 | Nova | 7,5 | 314,239 | 28,8741 | 262,450 | 376,247 |
| 5 | Nova | 10,0 | 272,783 | 30,6102 | 218,928 | 339,887 |